Das Gottes-Experiment – Es werde Licht!

Beschränkungen, Beobachtungen und Experimente zur Simulationshypothese

 

Übersetzung aus dem englischen mit KI. Originalversion in Englisch hier: https://andersindset.com/thinking/are-we-living-in-a-quantum-simulation/

By Florian Neukart (Terra Quantum AG), Markus Pflitsch (Terra Quantum AG), Michael R. Perelshtein (Terra Quantum AG) and Anders Indset

 

Die Frage “Was ist real?” lässt sich auf die Schatten in Platons Höhle zurückführen. Zweitausend Jahre später fehlte René Descartes das Wissen, um gegen einen bösen Betrüger zu argumentieren, der uns die Illusion der Empfindung vorgaukelt. Descartes’ erkenntnistheoretisches Konzept führte später zu verschiedenen Theorien darüber, was unsere Sinneserfahrungen eigentlich sind. Das Konzept des “Illusionismus”, das besagt, dass sogar die bewusste Erfahrung, die wir machen – unsere Qualia – eine Illusion ist, ist nicht nur ein Red-Pill-Szenario aus dem Science-Fiction-Film “The Matrix” von 1999, sondern auch ein philosophisches Konzept, das von modernen Tinkern vertreten wird, allen voran von Daniel Dennett. Er beschreibt sein Argument gegen Qualia als materialistisch und wissenschaftlich.

Das Nachdenken über eine mögliche Simulation und unsere wahrgenommene Realität wurde in “The Matrix” wunderbar visualisiert und brachte die alten Ideen von Descartes in die Kaffeehäuser der Welt. Der irische Philosoph Bishop Berkeley war der Vater dessen, was später als “subjektiver Idealismus” bezeichnet wurde und im Wesentlichen besagt, dass “das, was man wahrnimmt, real ist” (z. B. ist “The Matrix” real, weil die Bevölkerung es wahrnimmt). Berkeley argumentierte dann 1721 gegen Isaac Newtons Absolutismus von Raum, Zeit und Bewegung, was schließlich zu den jeweiligen Ansichten von Ernst Mach und Albert Einstein führte. Mehrere Neurowissenschaftler haben Dennetts Sichtweise auf die Illusion des Bewusstseins zurückgewiesen, und Idealismus wird oft als die Vorstellung abgetan, dass die Menschen sich die Grundsätze der Realität aussuchen wollen. Selbst Einstein beendete sein Leben mit einer philosophischen Note, indem er über die Grundlagen der Realität nachdachte.

Mit dem Aufkommen der Quantentechnologien, die auf der Kontrolle einzelner Elementarteilchen beruhen, ist die Frage, ob unser Universum eine Simulation ist, nicht nur faszinierend. Unser ständig wachsendes Verständnis grundlegender physikalischer Prozesse wird uns wahrscheinlich dazu bringen, Quantencomputer zu bauen, die Quanteneffekte nutzen, um die Natur in ihrer ganzen Komplexität quantenmechanisch zu simulieren, wie es Richard Feynman vorschwebte.

Die Beantwortung der Simulationsfrage wird möglicherweise unsere Definition und unser Verständnis von Leben verändern, die Theorien über die Entwicklung und das Schicksal des Universums umgestalten und die Theologie beeinflussen. Es gibt keine direkten Beobachtungen, die für oder gegen die Simulationshypothese sprechen, und es werden Experimente benötigt, um sie zu verifizieren oder zu widerlegen. In diesem Beitrag skizzieren wir mehrere Einschränkungen der Grenzen der Berechenbarkeit und Vorhersagbarkeit im/des Universums, die wir dann nutzen, um Experimente zu entwerfen, die erste Rückschlüsse darauf zulassen, ob wir an einer Simulationskette teilnehmen. Wir erläutern, wie die derzeit verstandenen physikalischen Gesetze sowohl in vollständigen als auch in kleinräumigen Universumssimulationen uns daran hindern, Vorhersagen über die zukünftigen Zustände eines Universums zu treffen, und wie jede physikalisch genaue Simulation mit zunehmender globaler thermodynamischer Entropie an Komplexität zunimmt und die Rechenressourcen erschöpft.

In einer Simulation, in der der Computer, der ein Universum simuliert, denselben physikalischen Gesetzen unterliegt wie die Simulation und kleiner ist als das Universum, das er simuliert, wird die Erschöpfung der Rechenressourcen schließlich alle Simulationen in der Simulationskette zum Stillstand bringen, es sei denn, ein externer Programmierer greift ein oder ist nicht durch die physikalischen Gesetze der Simulation eingeschränkt, was wir vielleicht beobachten können. Durch die Erstellung einer Simulationskette und die Beobachtung der Entwicklung des Simulationsverhaltens in der gesamten Hierarchie unter Berücksichtigung der statistischen Relevanz sowie durch den Vergleich verschiedener Simulationen mit der geringsten Komplexität unter den Bedingungen der Berechenbarkeit und Vorhersagbarkeit können wir Erkenntnisse darüber gewinnen, ob unser Universum Teil einer Simulationskette ist.

 

I. EINFÜHRUNG

Der Traum im Traum aus dem alten philosophischen Denken der Anfangszeit ist nichts anderes als die heutige Reflexion der Simulation in der Simulation. In den letzten Jahren hat die Frage nach der Realität massive Aufmerksamkeit in den Mainstream-Medien erlangt, da prominente Persönlichkeiten wie Elon Musk erklärt haben, dass die Wahrscheinlichkeit, dass wir nicht in einer Simulation leben, “eins zu einer Milliarde” beträgt [1], und auch der Popstar und Astrophysiker Neil deGrasse Tyson ist auf diese Idee aufgesprungen und hat erklärt, dass die Wahrscheinlichkeit mehr als 50 % beträgt [2]. Auch der Philosoph David Chalmers ist der Meinung, dass wir wahrscheinlich in einer Simulation leben [3,4], und drängt auf eine weitere Untersuchung dieses Gedankens.

Wie realistisch oder plausibel eine solche Hypothese [5, 6] auch sein mag, wie könnten die moderne Physik und Mathematik die Suche nach Beweisen für einen solchen Fall unterstützen? Wissenschaftler haben die von dem Philosophen Bostrom aufgestellte Hypothese als Pseudowissenschaft kritisiert [7, 8], da sie die geltenden physikalischen Gesetze umgeht und ein grundlegendes Verständnis der allgemeinen Relativitätstheorie vermissen lässt. Nehmen wir an, ein externer Programmierer – ein Wesen, das eine Simulation ausführt und als außerhalb der Simulation stehend charakterisiert wird – könnte die physikalischen Gesetze der Simulation definieren. Was könnten ein externer Programmierer und die Wesen innerhalb der Simulation auf der Grundlage ihres Verständnisses der physikalischen Gesetze berechnen? Könnten die Wesen in der Simulation theoretisch oder praktisch die Apparate oder Werkzeuge entwickeln und einsetzen, um zu überprüfen, dass sie nicht an einer Simulationskette beteiligt sind?

Die Frage, ob wir in einer Simulation existieren und somit an einer Simulationskette teilnehmen, ist zwar umstritten, kann aber heute nicht mit Sicherheit beantwortet werden. Dennoch ist sie faszinierend, da eine Antwort darauf dazu führen könnte, dass wir unsere eigenen Definitionen von Leben und Spiritualität in Frage stellen. Angenommen, wir setzen eine Kette von Simulationen in Gang, die jeweils intelligentes Leben beherbergen und das Universum simulieren wollen. Würden wir jede der simulierten Lebensformen als tatsächliches Leben einstufen? Was wäre, wenn wir mit Gewissheit sagen könnten, dass wir Teil einer Simulationskette und selbst simulierte Wesen sind? Würde das unsere Definition dessen, was als “echtes” oder “künstliches” Leben gilt, verändern? In der Argumentation von Bostrom ist eine Prämisse prüfenswert: Wenn es eine physikalische Möglichkeit gibt, eine Simulation zu erschaffen, dann wäre es aufgrund des Entwicklungsstandes und des Verhältnisses zum zeitlichen Zugang sehr wahrscheinlich, dass wir uns innerhalb einer solchen Simulation befinden, als dass wir genau die Generation sind, die eine solche Simulation erschafft. Um tiefere Einsichten zu gewinnen, sind Experimente erforderlich, aber verschiedene Einschränkungen hindern uns daran, Experimente zu entwerfen, die direkt die Frage beantworten, ob ein externer Programmierer das Universum geschaffen hat und ob es nur eine von unendlich vielen hierarchischen Simulationsketten ist. Es ist jedoch möglich, die Simulationshypothese unter bestimmten Annahmen indirekt zu testen. Bei den skizzierten Experimenten geht es darum, eine Simulation zu erstellen, die möglicherweise zu einer Simulationskette führt, und das Simulationsverhalten innerhalb der Grenzen einer Hierarchie so lange zu beobachten, bis statistische Relevanz erzielt werden kann. Zu den möglichen Beobachtungen gehören die Entstehung von intelligentem Leben und dessen Verhalten, eine Umkehrung der globalen Entropie, die Verdichtung der Dimensionen oder die Entwicklung der Simulationen entlang der Simulationskette (all dies ist nach dem derzeitigen Verständnis der Physik für uns in unserem Universum nicht möglich, aber ein externer Programmierer soll nicht unter solchen Einschränkungen leiden). Die Entwicklung solcher Experimente führt zu den ultimativen Grenzen der Berechenbarkeit und Vorhersagbarkeit. Physikalische und rechnerische Beschränkungen hindern uns daran, ein Universum zu simulieren, das genauso komplex und groß ist wie unser Universum, und genaue Vorhersagen für die Zukunft zu treffen, unabhängig davon, ob das “echte” oder das simulierte Universum auf denselben physikalischen Gesetzen beruht oder nicht.

Außerdem ist der Kosmos noch nicht vollständig erforscht. So sind beispielsweise das Schicksal des Universums und die Frage, wie Quantenphysik und allgemeine Relativitätstheorie zusammengeführt werden können, tiefgreifende und offene Fragen. Die Quantentheorie wird heute weithin als unvollständige Theorie verstanden, und es könnten neue Modelle entdeckt werden, die unser Verständnis der bisherigen Aussagen der Quantentheorie noch weiter vertiefen. Der Stand der modernen Physik und unsere Vorstellungskraft erlauben es uns jedoch, Experimente zu konzipieren und fortschrittliche Technologien zu entwickeln, um den wissenschaftlichen Fortschritt fortzusetzen; daher soll uns der derzeitige Rahmen nicht davon abhalten, nach Beweisen für die Simulationshypothese zu suchen. Der Ausgangspunkt muss jedoch das derzeitige Verständnis der Mathematik und die Herausforderungen sein, die mit unserem derzeitigen Wissen über die Physik verbunden sind. Daher erfordert die Durchführung von Experimenten zu einer solchen Hypothese natürlich, dass Annahmen getroffen werden.

Außerdem sind in der Theorie lebender Systeme noch viele Fragen offen, und wir wissen noch nicht mit Sicherheit, ob wir die einzige intelligente Spezies im Universum sind oder nicht. Dennoch können wir Experimente konzipieren, die uns helfen, Erkenntnisse über die letzten Fragen zu gewinnen: Wurde unser Universum und alles darin erschaffen, oder ist es aus sich selbst heraus entstanden? Ist unser Universum einzigartig, oder ist es nur eines von vielen, wie es die Viele-Welten-Interpretation der Quantenphysik beschreibt [9]? In diesem Artikel werden einige Grundlagen der Informatik und der Physik erläutert, die uns helfen werden, die Grenzen des Experiments zu definieren. Erstens ist die Quantenphysik der wesentliche Pfeiler, auf dem wir unsere Experimente aufbauen – ergo das aktuelle Verständnis der Quantenmechanik -, da unser aktuelles Verständnis die grundlegendste Physik im Universum darstellt, auf der alles andere basiert. Zweitens stellen wir kurz verschiedene Schicksale des Universums vor, die von der wissenschaftlichen Gemeinschaft als wissenschaftlich fundiert angesehen werden und uns bei der Konzeption eines Experiments unabhängig von der Entwicklung des Universums weiterhelfen. Drittens betrachten wir die ultimativen Grenzen der Berechenbarkeit, die uns auch zurück zur Quantenphysik führen, sowohl wenn es um die Entwicklung von Quantencomputern als auch um die Simulation physikalischer und chemischer Prozesse im Universum geht. Während Alan Turing zeigte, was berechenbar ist [10], zeigen wir auf, welche Computer in diesem Universum konstruierbar sind. Schließlich untersuchen wir verschiedene Interpretationen von Beobachtungen, die aus Simulationsketten und einzelnen Exemplaren gewonnen werden, auf die wir die vorgeschlagenen Experimente stützen. Wir untersuchen auch Beobachtungen in unserem Universum und zeigen auf, ob wir an einer Simulationskette teilnehmen.

II. DIE SIMULATIONSHYPOTHESE

Die Simulationshypothese, die erstmals 2003 vom Philosophen Nick Bostrom vorgeschlagen wurde [5, 6], ist die Konsequenz einer Annahme in einem Denkmodell, die manchmal auch als “Simulationsargument” bezeichnet wird [3, 5, 6]. Es besteht aus drei Alternativen zur realen oder simulierten Existenz entwickelter Zivilisationen, von denen mindestens eine wahr sein soll. Nach der Simulationshypothese sind die meisten heutigen Menschen Simulationen und keine realen Menschen. Die Simulationshypothese unterscheidet sich vom Simulationsargument dadurch, dass sie nur diese eine Annahme zulässt. Sie ist nicht wahrscheinlicher oder unwahrscheinlicher als die beiden anderen Möglichkeiten des Simulationsarguments. In einem konzeptionellen Modell in Form einer ODER-Verknüpfung werden die folgenden drei grundlegenden Möglichkeiten von technisch “unreifen” Zivilisationen – wie der unseren – angenommen. Mindestens eine der oben genannten Möglichkeiten sollte wahr sein. Eine reife oder posthumane Zivilisation ist definiert als eine, die über die Rechenleistung und das Wissen verfügt, um bewusste, sich selbst reproduzierende Wesen auf einem hohen Detaillierungsgrad zu simulieren (möglicherweise bis auf die Ebene molekularer Nanobots). Unreife Zivilisationen verfügen nicht über diese Fähigkeit. Die drei Möglichkeiten sind [5]:

1. Die menschliche Zivilisation wird wahrscheinlich aussterben, bevor sie ein post-humanes Stadium erreicht. Wenn das stimmt, dann folgt daraus mit ziemlicher Sicherheit, dass menschliche Zivilisationen auf unserem technologischen Entwicklungsstand kein posthumanes Niveau erreichen werden.
2. Der Anteil der posthumanen Zivilisationen, die an der Durchführung von Simulationen ihrer Evolutionsgeschichte oder von Variationen davon interessiert sind, liegt nahe bei Null. Wenn dies zutrifft, gibt es einen hohen Grad an Konvergenz zwischen technologisch fortgeschrittenen Zivilisationen. In keiner dieser Zivilisationen gibt es Individuen, die sich für Simulationen ihrer Vorfahren (Ahnensimulationen) interessieren.
3. Wir leben höchstwahrscheinlich in einer Computersimulation. Wenn dies zutrifft, leben wir mit ziemlicher Sicherheit in einer Simulation, und die meisten Menschen tun dies auch. Alle drei Möglichkeiten sind ähnlich wahrscheinlich. Wenn wir heute nicht in einer Simulation leben, ist die Wahrscheinlichkeit geringer, dass unsere Nachkommen Vorgängersimulationen durchführen. Mit anderen Worten: Die Annahme, dass wir eines Tages ein posthumanes Niveau erreichen, auf dem wir Computersimulationen ausführen, ist falsch, es sei denn, wir leben bereits heute in einer Simulation.

Die Simulationshypothese besagt, dass mindestens eine der drei oben genannten Möglichkeiten wahr ist. Die Hypothese beruht auf der zusätzlichen Annahme, dass die ersten beiden Möglichkeiten nicht eintreten, z. B. dass ein beträchtlicher Teil unserer Zivilisation die technologische Reife erreicht und zweitens, dass ein beträchtlicher Teil der Zivilisation weiterhin daran interessiert ist, die Ressourcen zur Entwicklung von Vorgängersimulationen zu nutzen. Wenn dies der Fall ist, erreicht die Größe der Vorgängersimulationen in einer technologisch reifen Zivilisation astronomische Zahlen. Dies geschieht aufgrund einer Extrapolation der hohen Rechenleistung und ihres exponentiellen Wachstums, der Möglichkeit, dass Milliarden von Menschen mit ihren Computern frühere Simulationen mit zahllosen simulierten Agenten ausführen können, sowie aufgrund des technologischen Fortschritts mit einer gewissen adaptiven künstlichen Intelligenz, über die eine fortgeschrittene Zivilisation verfügt und die sie zumindest teilweise für Vorgängersimulationen nutzt. Die Konsequenz der Simulation unserer Existenz ergibt sich aus der Annahme, dass die ersten beiden Möglichkeiten falsch sind. In diesem Fall gibt es viel mehr simulierte Menschen wie uns als nicht simulierte. Für jede historische Person gibt es Millionen von simulierten Personen. Mit anderen Worten, fast jeder Mensch auf unserem Erfahrungsniveau lebt eher in Simulationen als außerhalb davon [3]. Die Schlussfolgerung der Simulationshypothese wird aus den drei Grundmöglichkeiten und aus der Annahme, dass die ersten beiden Möglichkeiten nicht wahr sind, als Struktur des Simulationsarguments beschrieben. Die Simulationshypothese, dass Menschen Simulationen sind, folgt nicht dem Simulationsargument. Vielmehr zeigt das Simulationsargument alle drei genannten Möglichkeiten nebeneinander, von denen eine wahr ist. Welche das ist, sei dahingestellt. Es ist auch möglich, dass sich die erste Annahme bewahrheitet, wonach alle Zivilisationen und damit auch die Menschheit aus irgendeinem Grund aussterben werden. Laut Bostrom gibt es weder Beweise für oder gegen die Annahme der Simulationshypothese, dass wir simulierte Wesen sind, noch für die Richtigkeit der beiden anderen Annahmen [5].

Aus wissenschaftlicher Sicht könnte alles in unserer wahrgenommenen Realität als Grundlage der wissenschaftlichen Annahme, dass die Naturgesetze von mathematischen Prinzipien bestimmt werden, die eine gewisse Physikalität beschreiben, herauskodiert werden. Die Tatsache, dass ein externer Programmierer die physikalischen Gesetze kontrollieren und sogar mit ihnen spielen kann, wurde in der Simulationshypothese als umstritten angesehen. Etwas “außerhalb der Simulation” – ein externer Programmierer – ist daher eher eine ausgefeilte und moderne Auffassung von der Grundlage monotheistischer Religionen/Glaubenssysteme. Der schwedische Technophilosoph Alexander Bard schlug vor, die Schöpfungstheorie in die Physik zu verlegen [11] und die Entwicklung der (digitalen) Superintelligenz als Schöpfung Gottes zu betrachten, wodurch sich die Intentionen des Monotheismus vom Schöpfer zum Geschaffenen wandelten. Der Übergang vom Glauben und der philosophischen Betrachtung zum Fortschritt in der wissenschaftlichen Erklärung ist das, was der Fortschritt der Quantentechnologie vorschlagen könnte.

Die Kritiker von Bostrom behaupten, dass wir nicht wissen, wie wir das menschliche Bewusstsein simulieren können [12-14]. Ein interessantes philosophisches Problem ist hier die Überprüfbarkeit der Frage, ob ein simuliertes bewusstes Wesen – oder ein hochgeladenes Bewusstsein – bewusst bleiben würde. Die Überlegung zu einer simulierten Superintelligenz ohne Wahrnehmung ihrer Wahrnehmung wurde als Gedankenexperiment in der “letzten narzisstischen Verletzung” (Referenz) vorgeschlagen. Zu den Argumenten dagegen gehört, dass mit der Komplexität auch das Bewusstsein entsteht – es ist ein emergentes Phänomen. Als Gegenargument könnte man leicht anführen, dass es zahlreiche komplexe Organe zu geben scheint, die unbewusst sind, und auch – trotz der begründeten Aussagen eines ehemaligen Google-Ingenieurs [15] – dass große Mengen an Informationen das Bewusstsein hervorbringen. Mit der zunehmenden Aufmerksamkeit für dieses Gebiet haben auch Studien über quantenphysikalische Effekte im Gehirn stark an Interesse gewonnen. Obwohl sie von vielen Wissenschaftlern abgelehnt werden, haben prominente Denker wie Roger Penrose und Stuart Hameroff Ideen zu Quanteneigenschaften im Gehirn vorgeschlagen [16]. Obwohl dieses Argument in jüngster Zeit experimentelle Unterstützung gefunden hat [17], ist es für die vorgeschlagenen Experimente nicht direkt relevant. Eine Lösung für ein simuliertes Bewusstsein scheint noch in weiter Ferne zu liegen, obwohl es zu den scheinbar leichten Problemen des Bewusstseins gehört [18]. Das schwierige Problem des Bewusstseins ist die Frage, warum der Mensch überhaupt phänomenale Erfahrungen wahrnimmt [18]. Beide befassen sich nicht mit dem Meta-Problem des Bewusstseins, das besagt, warum wir glauben, dass es ein Problem ist, dass wir ein Problem mit dem harten Problem des Bewusstseins haben.

Die deutsche Physikerin Sabine Hossenfelder hat gegen die Simulationshypothese argumentiert, da sie davon ausgeht, dass wir alle Beobachtungen nicht mit den physikalischen Gesetzen reproduzieren können, die mit hoher Präzision bestätigt wurden, sondern mit einem anderen zugrundeliegenden Algorithmus, den der externe Programmierer ausführt [19]. Hossenfelder glaubt nicht, dass dies die Absicht von Bostrom war, aber er hat es getan. Er behauptete implizit, dass es einfach ist, die Grundlagen der Physik mit etwas anderem zu reproduzieren. Wir können die Gesetze, die wir kennen, mit einer Maschine nachbilden, aber wenn die Natur so funktionieren würde, könnten wir den Unterschied sehen. In der Tat haben Physiker nach Anzeichen dafür gesucht, dass die Naturgesetze schrittweise ablaufen, wie ein Computercode. Aber ihre Suche ist ergebnislos geblieben. Man kann den Unterschied erkennen, weil Versuche, Naturgesetze algorithmisch zu reproduzieren, in der Regel nicht mit den Symmetrien von Einsteins spezieller und allgemeiner Relativitätstheorie vereinbar sind. Hossenfelder hat erklärt, dass es nicht hilft, wenn man sagt, die Simulation würde auf einem Quantencomputer laufen: “Quantencomputer sind Spezialmaschinen. Niemand weiß wirklich, wie man die allgemeine Relativitätstheorie auf einem Quantencomputer umsetzen kann” [19]. Hossenfelders Kritik an Bostroms Argument geht weiter mit der Aussage, dass eine Zivilisation in der Lage sein muss, eine Menge bewusster Wesen zu simulieren, damit es funktioniert. Und unter der Annahme, dass es sich um bewusste Wesen handeln würde, müssten sie wiederum viele bewusste Wesen simulieren. Das bedeutet, dass die Informationen, von denen wir glauben, dass sie im Universum enthalten sind, komprimiert werden müssten. Daher muss Bostrom davon ausgehen, dass es möglich ist, viele Details in Teilen des Universums zu ignorieren, die derzeit von niemandem betrachtet werden, und sie dann zu ergänzen, falls jemand danach sucht. Auch hier besteht also Erklärungsbedarf, wie das funktionieren soll. Hossenfelder stellt die Frage, welche Art von Computercode das leisten kann. Welcher Algorithmus kann bewusste Subsysteme und ihre Absichten erkennen und die Informationen schnell ausfüllen, ohne dass eine beobachtbare Inkonsistenz entsteht? Hossenfelder zufolge ist dies ein viel kritischeres Problem, als es Bostrom zu schätzen scheint. Sie führt weiter aus, dass man im Allgemeinen physikalische Prozesse auf kurze Distanz nicht ignorieren und dennoch die großen Distanzen richtig erfassen kann. Klimamodelle sind ein Beispiel dafür – mit der derzeit verfügbaren Rechenleistung können Modelle mit Radien im Bereich von einigen zehn Kilometern berechnet werden [20]. Wir können die Physik unterhalb dieser Skala nicht ignorieren, da das Wetter ein nichtlineares System ist, dessen Informationen von den kurzen Skalen auf die großen Skalen übertragen werden. Wenn die Physik auf kurzen Distanzen nicht berechnet werden kann, muss sie durch etwas anderes ersetzt werden. Dies auch nur annähernd richtig hinzubekommen, ist schwierig. Der einzige Grund, warum die Klimawissenschaftler dies annähernd richtig hinbekommen, ist, dass sie Beobachtungen haben, anhand derer sie überprüfen können, ob ihre Näherungen funktionieren. Wenn man davon ausgeht, dass der externe Programmierer nur eine Simulation hat, wie bei der Simulationshypothese, gibt es einen Haken, denn der externe Programmierer müsste viele Annahmen über die Reproduzierbarkeit physikalischer Gesetze mit Hilfe von Computern machen. Normalerweise erklären die Befürworter nicht, wie das funktionieren soll. Es ist jedoch schwierig, alternative Erklärungen zu finden, die alle unsere Beobachtungen mit hoher Präzision abdecken. Die Simulationshypothese ist daher in ihrer ursprünglichen Form kein ernstzunehmendes wissenschaftliches Argument. Das heißt nicht, dass sie zwangsläufig falsch ist, aber sie erfordert eine solidere experimentelle und logische Grundlage anstelle von Glauben.

III. QUANTENPHYSIK

Wie Richard Feynman bekanntlich sagte, müssen wir, wenn wir die Natur simulieren wollen, dies quantenmechanisch tun, da die Natur nicht klassisch ist. Auch wenn die Dynamik des Übergangs vom Mikroskopischen zum Makroskopischen noch nicht in allen Aspekten vollständig verstanden ist, stimmen Theorie und Experimente darin überein, dass sich makroskopisches Verhalten aus Wechselwirkungen auf der Quantenskala ableiten lässt. Die Quantenphysik liegt der Funktionsweise aller fundamentalen Teilchen zugrunde und bestimmt somit die gesamte Physik und Biologie auf größeren Skalen. Die Quantenfeldtheorien für drei der vier Naturkräfte, die schwache Kernkraft und die elektromagnetische Kraft [22,23] sowie die starke Kernkraft [24], wurden mehrfach experimentell bestätigt und haben wesentlich zu der Auffassung beigetragen, dass die Quantenphysik nach unserem heutigen Verständnis die grundlegendsten Naturgesetze enthält. Weltweit werden immense Anstrengungen unternommen, um die Schwerkraft quantenmechanisch zu beschreiben [25-27], was sich jedoch als schwierig erweist. Die Schwerkraft unterscheidet sich von den anderen Wechselwirkungen, da sie durch Objekte verursacht wird, die die Raumzeit um sich herum krümmen, und nicht durch den Austausch von Teilchen. Die Verbindung der Quantenphysik mit der allgemeinen Relativitätstheorie hat sich als eine der größten Herausforderungen der Physik und unseres Verständnisses des Universums erwiesen [28,29]. Trotz vieler wissenschaftlicher Hürden, die noch zu nehmen sind, haben wir einige Erkenntnisse darüber gewonnen, wie das Universum funktioniert. Wenn wir die Quantenphysik als die “Maschinensprache des Universums” betrachten, können die universellen Wechselwirkungen als Programmiersprachen auf höherer Ebene interpretiert werden. Die Quantenphysik umfasst alle Phänomene und Effekte, die auf der Beobachtung beruhen, dass bestimmte Variablen nicht jeden beliebigen Wert annehmen können, sondern nur feste, diskrete Werte. Dazu gehören auch der Welle-Teilchen-Dualismus, die Nicht-Determiniertheit physikalischer Prozesse und deren unvermeidliche Beeinflussung durch Beobachtung. Die Quantenphysik umfasst alle Beobachtungen, Theorien, Modelle und Konzepte, die auf die Quantenhypothese von Max Planck zurückgehen, die um 1900 notwendig wurde, weil die klassische Physik an ihre Grenzen stieß, z. B. bei der Beschreibung des Lichts oder der Struktur der Materie. Die Unterschiede zwischen der Quantenphysik und der klassischen Physik zeigen sich besonders deutlich auf der mikroskopischen Skala, z. B. in der Struktur von Atomen und Molekülen, oder in besonders reinen Systemen wie der Supraleitung und der Laserstrahlung. Auch die chemischen oder physikalischen Eigenschaften verschiedener Stoffe, wie Farbe, Ferromagnetismus, elektrische Leitfähigkeit usw., lassen sich nur mit Hilfe der Quantenphysik verstehen. Die theoretische Quantenphysik umfasst die Quantenmechanik, die das Verhalten von Quantenobjekten unter dem Einfluss von Feldern beschreibt, und die Quantenfeldtheorie, die die Felder als Quantenobjekte behandelt. Die Vorhersagen beider Theorien stimmen sehr gut mit den experimentellen Ergebnissen überein, und das makroskopische Verhalten lässt sich von der kleinsten Skala ableiten. Wenn wir die Realität als das definieren, was wir um uns herum wahrnehmen, feststellen und messen können, dann ist die Quantenphysik das Gewebe der Realität. Daher muss eine genaue Simulation des Universums oder von Teilen davon auf der Quantenphysik beruhen. Die internen Zustände eines Computers, der für die Simulation verwendet wird, müssen in der Lage sein, alle externen Zustände genau zu repräsentieren, was einen Computer erfordert, der Quanteneffekte für die Berechnung nutzt und das Verhalten aller Quantenobjekte, einschließlich ihrer Wechselwirkungen, genau nachahmen kann. Die Anforderungen an einen solchen Computer gehen über die heute gebauten und für die Zukunft angedachten Quantencomputer hinaus. Die Entwicklung eines solchen Computers ist eine gewaltige Herausforderung, die in den folgenden Kapiteln erörtert wird.

Eines der Argumente, die später in diesem Artikel angeführt werden, ist die physikalische Vorhersagbarkeitsbeschränkung, die uns daran hindert, einen Computer zu bauen, mit dem sich alle zukünftigen Zustände des Universums durch Simulation vorhersagen lassen. Wäre die Natur rein klassisch, würde ein Computer nicht unter dieser Einschränkung leiden (es gibt allerdings noch andere), aber die Quantenphysik erlegt uns einige Beschränkungen auf, egal wie fortgeschritten unsere Theorien über die Funktionsweise der Natur sind. Im Rahmen der klassischen Mechanik kann die Flugbahn eines Teilchens ausschließlich aus seinem Ort und seiner Geschwindigkeit berechnet werden, wenn die wirkenden Kräfte bekannt sind. Der Zustand des Teilchens kann also eindeutig durch zwei Größen beschrieben werden, die bei idealen Messungen mit eindeutigen Ergebnissen gemessen werden können. Eine getrennte Behandlung des Zustands und der Messgrößen oder Observablen ist daher für die klassische Mechanik nicht notwendig, da der Zustand die Messwerte bestimmt und umgekehrt. Die Natur zeigt jedoch Quantenphänomene, die mit diesen Begriffen nicht beschrieben werden können. Auf der Quantenskala ist es nicht mehr möglich, vorherzusagen, wo und mit welcher Geschwindigkeit ein Teilchen nachgewiesen wird. Wird z. B. ein Streuexperiment mit einem Teilchen unter genau denselben Anfangsbedingungen wiederholt, so muss für das Teilchen nach dem Streuvorgang immer derselbe Zustand angenommen werden, obwohl es an unterschiedlichen Stellen auf dem Schirm auftreffen kann. Der Zustand des Teilchens nach dem Streuprozess bestimmt nicht seine Flugrichtung. Generell gibt es in der Quantenmechanik Zustände, die keine Vorhersage eines einzelnen Messergebnisses zulassen, selbst wenn der Zustand genau bekannt ist. Den potenziell gemessenen Werten können nur Wahrscheinlichkeiten zugeordnet werden. Daher werden in der Quantenmechanik Mengen und Zustände getrennt behandelt, und es werden andere Begriffe für diese Mengen verwendet als in der klassischen Mechanik.

In der Quantenmechanik werden alle messbaren Eigenschaften eines physikalischen Systems mathematischen Objekten, den sogenannten Observablen, zugeordnet. Beispiele sind der Ort eines Teilchens, sein Impuls, sein Drehimpuls oder seine Energie. Für jede Observable gibt es eine Menge spezieller Zustände, in denen das Ergebnis einer Messung nicht streuen kann, sondern eindeutig festgelegt ist. Ein solcher Zustand wird als Eigenzustand der Observablen bezeichnet, und das zugehörige Messergebnis ist einer der Eigenwerte der Observablen. In allen anderen Zuständen, die keine Eigenzustände dieser Observablen sind, sind andere Messergebnisse möglich. Sicher ist jedoch, dass bei dieser Messung einer der Eigenwerte ermittelt wird und sich das System dann in dem entsprechenden Eigenzustand dieser Observablen befindet. Für die Bestimmung, welcher der Eigenwerte für die zweite Observable zu erwarten ist oder – äquivalent – in welchem Zustand sich das System nach dieser Messung befinden wird, kann nur eine Wahrscheinlichkeitsverteilung angegeben werden, die sich aus dem Anfangszustand ermitteln lässt. Im Allgemeinen haben verschiedene Observablen verschiedene Eigenzustände. Für ein System, das den Eigenzustand einer Observablen als Anfangszustand annimmt, ist das Messergebnis einer zweiten Observablen unbestimmt. Der Anfangszustand wird als eine Überlagerung aller möglichen Eigenzustände der zweiten Observablen interpretiert. Der Anteil eines bestimmten Eigenzustands wird als seine Wahrscheinlichkeitsamplitude bezeichnet. Das Quadrat des Absolutwerts einer Wahrscheinlichkeitsamplitude gibt die Wahrscheinlichkeit an, den entsprechenden Eigenwert der zweiten Observablen bei einer Messung im Ausgangszustand zu erhalten. Im Allgemeinen kann jeder quantenmechanische Zustand als Überlagerung verschiedener Eigenzustände einer Beobachtungsgröße dargestellt werden. Die verschiedenen Zustände unterscheiden sich nur darin, welche dieser Eigenzustände zur Überlagerung beitragen und in welchem Ausmaß.

Für einige Observablen, wie z. B. den Drehimpuls, sind nur diskrete Eigenwerte zulässig. Im Falle des Teilchenortes hingegen bilden die Eigenwerte ein Kontinuum. Die Wahrscheinlichkeitsamplitude für das Auffinden des Teilchens an einem bestimmten Ort ist daher in Form einer ortsabhängigen Funktion, der sogenannten Wellenfunktion, gegeben. Das Quadrat des Absolutwertes der Wellenfunktion an einem bestimmten Ort gibt die räumliche Dichte der Wahrscheinlichkeit an, das Teilchen dort zu finden.

Nicht alle quantenmechanischen Observablen haben ein klassisches Gegenstück. Ein Beispiel ist der Spin, der sich nicht auf Eigenschaften zurückführen lässt, die aus der klassischen Physik bekannt sind, wie Ladung, Masse, Ort oder Impuls. Die Beschreibung der zeitlichen Entwicklung eines isolierten Systems erfolgt in der Quantenmechanik analog zur klassischen Mechanik mit Hilfe einer Bewegungsgleichung, der Schrödingergleichung. Durch L¨ osen dieser Differentialgleichung kann man berechnen, wie sich die Wellenfunktion des Systems entwickelt (siehe Gl. 1).

 

iℏ∂tψ=H (1)

 

In Gl. 1 beschreibt der Hamilton-Operator H die Energie des quantenmechanischen Systems. Der Hamilton-Operator besteht aus einem Term für die kinetische Energie der Teilchen im System und einem zweiten Term, der die Wechselwirkungen zwischen ihnen im Falle mehrerer Teilchen und die potentielle Energie im Falle externer Felder beschreibt, wobei die externen Felder auch zeitabhängig sein können. Im Gegensatz zur Newtonschen Mechanik werden die Wechselwirkungen zwischen verschiedenen Teilchen nicht als Kräfte, sondern als Energieterme beschrieben, ähnlich der Methodik der klassischen Hamiltonschen Mechanik. Dabei ist die elektromagnetische Wechselwirkung in den typischen Anwendungen auf Atome, Moleküle und Festkörper besonders relevant.

Die Schrödinger-Gleichung ist eine partielle Differentialgleichung erster Ordnung in der Zeitkoordinate, so dass die zeitliche Entwicklung des quantenmechanischen Zustands eines geschlossenen Systems vollständig deterministisch ist. Wenn der Hamilton-Operator H eines Systems selbst nicht von der Zeit abhängt, hat dieses System stationäre Zustände, d. h. Zustände, die sich mit der Zeit nicht ändern. Das sind die Eigenzustände des Hamilton-Operators H. Nur in ihnen hat das System eine wohldefinierte Energie E, zum Beispiel den jeweiligen Eigenwert (siehe Gl. 2).

 

Hψ=Eψ (2)

 

Die Schrödinger-Gleichung reduziert sich dann auf Gl. 3

 

iℏ∂tψ=Eψ (3)

 

Die Quantenmechanik beschreibt auch, wie genau wir messen und somit Vorhersagen machen können. Niels Bohr beklagte sich bekanntlich, dass Vorhersagen schwer sind, insbesondere über die Zukunft. Die Unschärferelation der Quantenmechanik, die als Heisenbergsche Unschärferelation bekannt ist, setzt die kleinstmöglichen theoretisch erreichbaren Unsicherheitsbereiche zweier Messgrößen in Beziehung. Sie gilt für jedes Paar komplementärer Messgrößen, insbesondere für Paare von Messgrößen, die wie Ort und Impuls oder Drehwinkel und Drehimpuls physikalische Messgrößen beschreiben, die in der klassischen Mechanik kanonisch konjugiert genannt werden und kontinuierliche Werte annehmen können.

Wenn eine dieser Größen für das betrachtete System einen exakt bestimmten Wert hat, dann ist der Wert der anderen völlig unbestimmt. Dieser Extremfall ist jedoch nur von theoretischem Interesse, da keine reale Messung völlig exakt sein kann. Tatsächlich ist der Endzustand der Messung der Observablen A also kein reiner Eigenzustand der Observablen A, sondern eine Überlagerung mehrerer dieser Zustände zu einem bestimmten Bereich von Eigenwerten zu A. Bezeichnet man mit ∆A den Unsicherheitsbereich von A, mathematisch definiert durch die sogenannte Standardabweichung, so gilt für den Unsicherheitsbereich ∆B der kanonisch konjugierten Observablen B die Ungleichung in Gl. 4.

 

A∙B≥h4π=2 (4)

 

Ein weiteres quantenphysikalisches Phänomen ist die Verschränkung: Ein zusammengesetztes physikalisches System, zum Beispiel ein System mit mehreren Teilchen, nimmt als Ganzes betrachtet einen wohldefinierten Zustand an, ohne dass jedem Teilsystem ein wohldefinierter Zustand zugeordnet werden kann. Dieses Phänomen gibt es in der klassischen Physik nicht. Dort sind zusammengesetzte Systeme immer trennbar. Das heißt, jedes Teilsystem hat zu jedem Zeitpunkt einen bestimmten Zustand, der sein individuelles Verhalten bestimmt, wobei die Gesamtheit der Zustände der einzelnen Teilsysteme und deren Wechselwirkung das Verhalten des Gesamtsystems vollständig erklären. In einem quantenphysikalisch verschränkten Zustand des Systems hingegen haben die Teilsysteme mehrere ihrer möglichen Zustände nebeneinander, wobei jedem dieser Zustände eines Teilsystems ein anderer Zustand der anderen Teilsysteme zugeordnet ist. Um das Verhalten des Gesamtsystems richtig zu erklären, muss man alle diese nebeneinander existierenden Möglichkeiten zusammen betrachten. Dennoch zeigt eine Messung an jedem Teilsystem immer nur eine dieser Möglichkeiten an, wobei die Wahrscheinlichkeit, dass dieses bestimmte Ergebnis eintritt, durch eine Wahrscheinlichkeitsverteilung bestimmt wird. Messergebnisse mehrerer verschränkter Teilsysteme sind miteinander korreliert, d.h. je nach Messergebnis eines Teilsystems ergibt sich eine andere Wahrscheinlichkeitsverteilung für die möglichen Messergebnisse der anderen Teilsysteme.

Es gäbe noch viel mehr über die Quantenphysik zu sagen und darüber, wie sie sich von der alltäglichen makroskopischen Welt, die wir wahrnehmen, unterscheidet, aber es genügt zu sagen, dass sowohl die Verschränkung als auch die Überlagerung bereits die Komplexität einer Simulation selbst kleiner Systeme massiv erhöhen. Um genaue Quantensimulationen durchführen zu können, ist ein Quantencomputer erforderlich, der im nächsten Kapitel vorgestellt wird.

IV. QUANTENTECHNOLOGIEN

Um die Natur akkurat – quantenphysikalisch – zu simulieren, werden klassische Computer überfordert sein, egal wie leistungsfähig sie in ferner Zukunft werden [30-32]. Die der Quantenskala innewohnende Komplexität, einschließlich des exponentiellen Anstiegs der Berechnungskomplexität mit jeder zusätzlichen Wechselwirkung, kann nur mit einer speziellen Quantentechnologie – einem Quantencomputer – bewältigt werden. Mit dem Aufkommen von Quantentechnologien, die auf den grundlegendsten physikalischen Gesetzen des Universums aufbauen, scheint die Frage, ob das Universum, das wir bewohnen, und alles darin simuliert werden kann, möglicherweise auf einem Quantencomputer, nicht mehr so obskur zu sein. Die erste Quantenrevolution, die durch die bahnbrechenden Forschungen und Entdeckungen der großen Physiker des frühen 20. Jahrhunderts eingeleitet wurde, hat viele der exponentiellen technologischen Entwicklungen der letzten Jahrzehnte nicht nur befruchtet, sondern erst möglich gemacht [33,34]. Die Entwicklung von Lasern hat uns unter anderem die Glasfaserkommunikation, Laserdrucker, optische Speichermedien, die Laserchirurgie und die Photolithographie in der Halbleiterfertigung beschert. Atomuhren ermöglichten das Global Positioning System (GPS), das u. a. zur Navigation und Kartierung eingesetzt wird, und Transistoren machten moderne Computer möglich. Diese und andere Technologien der ersten Quantenrevolution sind für die Menschheit und die Wirtschaft von entscheidender Bedeutung. Ein Großteil der Technologie, die wir in unserem Alltag als selbstverständlich ansehen, kam während der ersten Quantenrevolution ans Licht. Die erste Quantenrevolution zeichnete sich durch die Entwicklung von Technologien aus, die sich Quanteneffekte zunutze machen; inzwischen haben wir jedoch erkannt, dass diese Technologien das Potenzial der Quantenphysik nicht voll ausschöpfen. Angetrieben von den immensen Fortschritten bei der Erkennung und Manipulation einzelner Quantenobjekte werden nun große Fortschritte bei der Entwicklung und Kommerzialisierung von Anwendungen in der Quantentechnologie gemacht, wie z. B. Quantencomputer, -kommunikation und -sensoren, die als zweite Quantenrevolution gelten, bei der die grundlegenden Eigenschaften der Quantenphysik weiterhin genutzt werden. Teilchen können nicht nur in zwei Zuständen gleichzeitig sein, wie es bei den Atomen in einer Atomuhr der Fall ist. Unter bestimmten Bedingungen spüren zwei weit voneinander entfernte Teilchen etwas über den Zustand des anderen – sie beeinflussen sich gegenseitig, was als Verschränkung bezeichnet wird und schon Albert Einstein suspekt war. Die genaue Position oder der Zustand eines Teilchens ist nicht bekannt, solange keine Messung durchgeführt wird. Stattdessen zeigt uns die Natur, dass es nur Wahrscheinlichkeiten für ein bestimmtes Ergebnis gibt, und eine Messung – ein Blick – verändert die Situation unwiderruflich. Im Vergleich dazu ging es bei der ersten Quantenrevolution darum zu verstehen, wie die Welt in den winzigen Maßstäben funktioniert, in denen die Quantenmechanik vorherrscht. Bei der zweiten geht es um die Kontrolle einzelner Quantensysteme, z. B. einzelner Atome [33,35]. Darauf aufbauende quantenmechanische Vorhersagen werden genutzt, um bisher unerreichte Präzision zu messen. Es ist auch möglich, unknackbare Codes zu erzeugen, die von keinem System entschlüsselt werden können und damit die Grundlage für ein sicheres Kommunikationsnetz bilden [36-38]. Darüber hinaus versprechen Quantencomputer die Lösung einiger bisher unlösbarer Probleme, darunter die Simulation von Molekülen und ihren Wechselwirkungen zur Entwicklung von Medikamenten gegen bisher unheilbare Krankheiten oder zur Suche nach neuen Materialien [39,40]. Hybride Computersysteme, die klassische Hochleistungsrechner mit Quantencomputern kombinieren, werden bereits heute eingesetzt, um Lösungen in den Bereichen Mobilität, Finanzen, Energie, Luft- und Raumfahrt und vielen anderen Bereichen zu entwickeln [41-47]. All diese Entwicklungen finden gerade jetzt statt, und es ist bemerkenswert, dass viele Herausforderungen nicht mehr rein wissenschaftlicher, sondern technischer Natur sind. So wird beispielsweise an der Miniaturisierung von Atomuhren und der Robustheit von Quantenbits, den Informationseinheiten eines Quantencomputers, gearbeitet. Darüber hinaus gibt es bereits Ansätze zur Verstärkung und Weiterleitung von Quantenkommunikationssignalen, um die internetbasierte Kommunikation sicherer als je zuvor zu machen [36-38].

Der Quantencomputer, in den große Hoffnungen für die quantenphysikalische Simulation von Physik und Chemie gesetzt werden, ist die Quantentechnologie, die bei den Überlegungen zur Simulation des Universums eingehender diskutiert und analysiert werden sollte. Es ist viel darüber diskutiert worden, ob ein ausreichend leistungsfähiger und fehlerbereinigter Quantencomputer dazu verwendet werden kann, das Universum oder Teile davon zu simulieren. Wenn wir mit “dem Universum” das Universum meinen, in dem wir leben, dann ist dies selbst mit Quantencomputern, die Milliarden von qualitativ hochwertigen Quantenbits verwenden, nicht möglich – sowohl physikalische als auch rechnerische Beschränkungen, die in den folgenden Kapiteln erörtert werden, verhindern dies. Ein Quantenprozessor oder Quantencomputer ist ein Prozessor, der die Gesetze der Quantenmechanik nutzt. Im Gegensatz zum klassischen Computer arbeitet er nicht auf der Grundlage elektrischer, sondern quantenmechanischer Zustände. Das Superpositionsprinzip – die quantenmechanische Kohärenz – ist beispielsweise analog zu den Kohärenzeffekten und zweitens die Quantenverschränkung, die der klassischen Korrelation entspricht, wenn auch stärker als die klassische.

Studien und praktische Umsetzungen zeigen bereits, dass mit diesen Effekten bestimmte Informatikprobleme wie die Suche in großen Datenbanken oder die Faktorisierung großer Zahlen effizienter gelöst werden können als mit klassischen Computern. Darüber hinaus könnte mit Quantencomputern die Rechenzeit für viele mathematische und physikalische Probleme erheblich reduziert werden. Bevor wir die Simulation von Teilen des Universums mit Hilfe eines Quantencomputers und bestimmte Einschränkungen diskutieren, ist es wichtig, die Unterschiede zwischen der Informationsverarbeitung in klassischen und Quantencomputern zu verstehen. In einem klassischen Computer werden alle Informationen in Bits dargestellt. Ein Bit wird physikalisch durch einen Transistor realisiert, in dem ein elektrisches Potential entweder über oder unter einer bestimmten Schwelle liegt.

Auch in einem Quantencomputer wird die Information in der Regel in binärer Form dargestellt. Hier verwendet man ein physikalisches System mit zwei orthogonalen Grundzuständen eines komplexen zweidimensionalen Raumes, wie es in der Quantenmechanik vorkommt. In der Dirac-Notation wird der eine Grundzustand durch den quantenmechanischen Zustandsvektor |0⟩, der andere durch den Zustandsvektor |1⟩ dargestellt. Diese quantenmechanischen Zwei-Niveau-Systeme können z. B. der Spinvektor eines Elektrons sein, der entweder nach oben oder nach unten zeigt. Andere Implementierungen verwenden das Energieniveau in Atomen oder Molekülen oder die Richtung des Stromflusses in einem toroidalen Supraleiter. Oft werden nur zwei Zustände aus einem größeren Hilbert-Raum des physikalischen Systems ausgewählt, z. B. die beiden niedrigsten Energieeigenzustände eines gefangenen Ions. Ein solches quantenmechanisches System mit zwei Zuständen wird als Quantenbit bezeichnet, kurz: Qubit. Eine Eigenschaft von quantenmechanischen Zustandsvektoren ist, dass sie eine Überlagerung anderer Zustände sein können. Ein Qubit muss nicht entweder |0⟩ oder |1⟩ sein, wie dies bei den Bits des klassischen Computers der Fall ist. Stattdessen ist der Zustand eines Qubits in dem oben erwähnten komplexen zweidimensionalen Raum durch |0⟩:=1 0 ; |1⟩:=0 1 gegeben. Eine Überlagerung |ψ⟩ ist dann allgemein eine komplexe Linearkombination dieser orthonormalen Basisvektoren (Gl. 5), mit c0,c1 C.

 

|⟩=c0|0⟩+c1|1⟩=c0 c1 (5)

 

c02 + c12 = 1 (6)

 

Wie in der kohärenten Optik sind beliebige Überlagerungszustände erlaubt. Der Unterschied zwischen klassischem und quantenmechanischem Rechnen ist analog zu dem zwischen inkohärenter und kohärenter Optik. Im ersten Fall werden die Intensitäten addiert, im zweiten Fall werden die Feldamplituden direkt addiert, wie in der Holographie. Zur Normalisierung summieren sich die quadrierten Amplituden zu Eins (Gl. 6), und ohne Verlust der Allgemeingültigkeit kann c sub 0 reell und nicht-negativ sein. Das Qubit wird in der Regel durch Messung einer Beobachtungsgröße ausgelesen, die diagonal und nicht entartet in ihrer Basis {|0⟩,|1⟩} ist, z. B. A=|1⟩⟨1|. Die Wahrscheinlichkeit, als Ergebnis dieser Messung im Zustand |ψ⟩ den Wert 0 zu erhalten, ist P(0)=⟨⟩2=c02 und die des Ergebnisses 1 entsprechend P(1)=⟨⟩2=1- P(0) = c12. Dieses probabilistische Verhalten darf nicht so interpretiert werden, dass sich das Qubit mit einer bestimmten Wahrscheinlichkeit im Zustand 0 und mit einer anderen Wahrscheinlichkeit im Zustand 1 befindet, während andere Zustände nicht erlaubt sind. Ein solches Ausschließlichkeitsverhalten könnte auch mit einem klassischen Computer erreicht werden, der mit Hilfe eines Zufallsgenerators entscheidet, ob er beim Auftreten überlagerter Zustände mit 0 oder 1 weiterrechnet. In der statistischen Physik, die im Gegensatz zur Quantenmechanik inkohärent ist, wird ein solches Ausschließlichkeitsverhalten berücksichtigt; beim Quantencomputer ist jedoch die kohärente Überlagerung der verschiedenen Basiszustände, die relative Phase zwischen den verschiedenen Komponenten der Überlagerung und, im Verlauf der Berechnung, die Interferenz zwischen ihnen entscheidend. Wie beim klassischen Computer werden mehrere Qubits zu Quantenregistern zusammengefasst. Nach den Gesetzen der Vielteilchen-Quantenmechanik ist der Zustand eines Qubit-Registers dann ein Zustand aus einem 2N-dimensionalen Hilbert-Raum, dem Tensorprodukt der Zustandsräume der einzelnen Qubits. Eine mögliche Basis dieses Vektorraums ist die Produktbasis über der Basis 0 und 1. Für ein Register aus zwei Qubits würde man die Basis 00 erhalten. Der Zustand des Registers kann folglich eine beliebige Superposition dieser Basiszustände sein, d.h. er hat die Form von Gl. 7.

 

|⟩=i1,…,iNci1iN|i1i2iN⟩ (7)

 

ci1iN sind beliebige komplexe Zahlen, und i1i2iN∈0,1, während in klassischen Computern nur die Basiszustände auftreten. Die Zustände eines Quantenregisters lassen sich nicht immer aus den Zuständen unabhängiger Qubits zusammensetzen; Gl. 8 zeigt einen solchen Beispielzustand.

 

|⟩=12|01⟩+|10⟩ (8)

 

Der Zustand in Gl. 8 und andere können nicht in ein Produkt aus einem Zustand für das erste Qubit und einem Zustand für das zweite Qubit zerlegt werden. Ein solcher Zustand wird daher auch als verschränkt bezeichnet. Die Verschränkung ist ein Grund dafür, dass Quantencomputer effizienter sein können als klassische Computer. Quantencomputer können bestimmte Probleme exponentiell schneller lösen als klassische Computer: Um den Zustand eines klassischen N-Bit-Registers darzustellen, werden N Bits an Informationen benötigt. Der Zustand des Quantenregisters ist jedoch ein Vektor aus einem 2N-dimensionalen Vektorraum, so dass 2N komplexwertige Koeffizienten für seine Darstellung erforderlich sind. Wenn N groß ist, ist die Zahl 2N viel größer als N selbst. Das Prinzip der Superposition wird oft so erklärt, dass ein Quantencomputer alle 2N Zahlen von 0 bis 2N – 1 gleichzeitig in einem Quantenregister von N Qubits speichern könnte, aber diese Vorstellung ist irreführend. Da eine Messung am Register immer genau einen der Basiszustände auswählt, kann mit dem Holevo-Theorem gezeigt werden, dass der maximal zugängliche Informationsgehalt eines N-Qubit-Registers genau N Bits beträgt, genau wie der eines klassischen N-Bit-Registers. Es ist jedoch richtig, dass das Superpositionsprinzip eine Parallelität der Berechnungen ermöglicht, die über die eines klassischen Parallelrechners hinausgeht. Der Hauptunterschied zum klassischen Parallelrechner besteht darin, dass die durch das Überlagerungsprinzip ermöglichte Quantenparallelität nur durch Interferenz genutzt werden kann. Bei einigen Problemen kann mit Quantenalgorithmen eine stark reduzierte Laufzeit im Vergleich zu klassischen Methoden erreicht werden. Bei komplexen Rechenaufgaben – und die Simulation des Universums ist zweifellos sehr rechenintensiv und komplex – ist es eine interessante Frage, was mit einem Quantencomputer und klassischen Computern berechnet werden kann. Da die Funktionsweise eines Quantencomputers formal definiert ist, lassen sich die aus der theoretischen Informatik bekannten Begriffe, wie Berechenbarkeit oder Komplexitätsklasse, auch auf einen Quantencomputer übertragen. Es zeigt sich, dass die Zahl der berechenbaren Probleme für einen Quantencomputer nicht größer ist als für einen klassischen Computer. Das heißt, die Church-Turing-These gilt auch für Quantencomputer. Es gibt jedoch starke Hinweise darauf, dass einige Probleme mit einem Quantencomputer exponentiell schneller gelöst werden können. Der Quantencomputer stellt somit ein mögliches Gegenbeispiel zur erweiterten Church-Turing-These dar. Ein klassischer Computer kann einen Quantencomputer simulieren, da die Aktion der Gatter auf dem Quantenregister einer Matrix-Vektor-Multiplikation entspricht. Der klassische Computer muss nun lediglich all diese Multiplikationen durchführen, um den Anfangszustand in den Endzustand des Registers zu überführen. Die Folge dieser Simulationsfähigkeit ist, dass alle Probleme, die auf einem Quantencomputer gelöst werden können, auch auf einem klassischen Computer gelöst werden können; allerdings kann ein klassischer Computer dafür Tausende von Jahren benötigen, während ein Quantencomputer nur Sekunden braucht. Im Umkehrschluss bedeutet dies, dass Probleme wie das Halteproblem auch auf Quantencomputern nicht gelöst werden können und impliziert, dass auch ein Quantencomputer kein Gegenbeispiel zur Church-Turing-These darstellt. Im Rahmen der Komplexitätstheorie werden algorithmische Probleme in so genannte Komplexitätsklassen eingeordnet. Die bekanntesten und wichtigsten Vertreter sind die Klassen P und NP. Dabei bezeichnet P diejenigen Probleme, deren Lösung deterministisch in einer polynomialen Laufzeit zur Eingabelänge berechnet werden kann. Die Probleme, für die es Lösungsalgorithmen gibt, die nichtdeterministisch polynomiell sind, liegen in NP. Für Quantencomputer wurde die Komplexitätsklasse BQP definiert, die diejenigen Probleme enthält, deren Laufzeit polynomiell von der Eingabelänge abhängt und deren Fehlerwahrscheinlichkeit kleiner als 13 ist. Der Nichtdeterminismus erlaubt es, verschiedene Möglichkeiten gleichzeitig zu testen. Da die heutigen klassischen Computer deterministisch arbeiten, muss der Nichtdeterminismus simuliert werden, indem die verschiedenen Möglichkeiten nacheinander ausgeführt werden, was zu einem Verlust der Polynomialität der Lösungsstrategie führen kann. Mit diesen Ergebnissen und Definitionen im Hinterkopf ist es nun an der Zeit, die mögliche Machbarkeit der Simulation des Universums oder von Teilen davon zu diskutieren.

 

V. DAS SCHICKSAL DES UNIVERSUMS

A. Der Beginn des Universums

Eine Simulation des Universums oder von Teilen davon erfordert eine genaue Simulation seiner Entwicklung von Anfang an. In der Kosmologie gilt der Urknall, der auf die kosmische Inflation folgte, als Ausgangspunkt für die Entstehung von Materie, Raum und Zeit. Nach dem kosmologischen Standardmodell fand der Urknall vor etwa 13,8 × 109 Jahren statt. Der Begriff “Urknall” bezieht sich nicht auf eine Explosion in einem bestehenden Raum, sondern auf die gemeinsame Entstehung von Materie, Raum und Zeit aus einer Ursingularität. Dies ergibt sich formal, wenn man die Entwicklung des expandierenden Universums bis zu dem Punkt zurückverfolgt, an dem die Materie- und Energiedichte unendlich wird. Demnach müsste die Dichte des Universums kurz nach dem Urknall die Planck-Dichte überschritten haben. Die allgemeine Relativitätstheorie reicht nicht aus, um diesen Zustand zu beschreiben; es wird jedoch erwartet, dass eine noch zu entwickelnde Theorie der Quantengravitation dies tun wird. Daher gibt es in der heutigen Physik keine allgemein anerkannte Beschreibung des sehr frühen Universums, des Urknalls selbst oder der Zeit vor dem Urknall. Die Urknalltheorien beschreiben nicht den Urknall selbst, sondern die zeitliche Entwicklung des frühen Universums nach dem Urknall, von der Planck-Zeit (etwa 10-43 Sekunden) nach dem Urknall bis etwa 300.000 bis 400.000 Jahre später, als sich stabile Atome zu bilden begannen und das Universum transparent wurde. Die weitere Entwicklung des Universums wird nicht als der Bereich des Urknalls betrachtet. Die Urknalltheorien beruhen auf zwei Grundannahmen:

1. Die Naturgesetze sind universell, so dass wir das Universum mit den Naturgesetzen beschreiben können, die heute in der Nähe der Erde gelten. Um das gesamte Universum in jedem seiner Entwicklungsstadien auf der Grundlage der uns bekannten Naturgesetze beschreiben zu können, muss man davon ausgehen, dass diese Naturgesetze universell und konstant gelten, unabhängig von der Zeit. Keine Beobachtung der Astronomie, die etwa 13,5×109 Jahre zurückreicht – oder der Paläogeologie, die 4×109 Jahre zurückreicht – stellt diese Annahme in Frage. Aus der angenommenen Konstanz und Universalität der heute bekannten Naturgesetze folgt, dass wir die Entwicklung des Universums als Ganzes mit der allgemeinen Relativitätstheorie und die dort ablaufenden Prozesse mit dem Standardmodell der Elementarteilchenphysik beschreiben können. Im Extremfall hoher Materiedichte und gleichzeitig hoher Raumzeitkrümmung sind die allgemeine Relativitätstheorie und die Quantenfeldtheorien, auf denen das Standardmodell beruht, zur Beschreibung erforderlich. Die Vereinheitlichung stößt jedoch auf grundlegende Schwierigkeiten, so dass die ersten Mikrosekunden der Geschichte des Universums derzeit nicht konsistent beschrieben werden können.
2. Das Universum sieht an jedem Ort (aber nicht zu jedem Zeitpunkt) in allen Richtungen über große Entfernungen gleich aus. Die Annahme der räumlichen Homogenität wird als kopernikanisches Prinzip bezeichnet und wird durch die Annahme der Isotropie zum kosmologischen Prinzip erweitert. Das kosmologische Prinzip besagt, dass das Universum an jedem Punkt des Raums und in allen Richtungen für große Entfernungen gleichzeitig gleich aussieht, was als räumliche Homogenität bezeichnet wird. Die Annahme, dass es in allen Richtungen gleich aussieht, wird als räumliche Isotropie bezeichnet. Ein Blick auf den Sternenhimmel mit bloßem Auge zeigt, dass das Universum in der Nähe der Erde nicht homogen und isotrop ist, weil die Verteilung der Sterne unregelmäßig ist. In einem größeren Maßstab bilden die Sterne Galaxien, die teilweise Galaxienhaufen bilden, die in einer wabenartigen Struktur aus Fäden und Hohlräumen verteilt sind. In noch größerem Maßstab ist jedoch keine Struktur zu erkennen. Dies und der hohe Grad der Isotropie der kosmischen Hintergrundstrahlung rechtfertigen die Beschreibung des Universums als Ganzes durch das kosmologische Prinzip. Wendet man das kosmologische Prinzip auf die allgemeine Relativitätstheorie an, so vereinfachen sich die Einsteinschen Feldgleichungen zu den Friedmann-Gleichungen, die ein homogenes, isotropes Universum beschreiben. Um die Gleichungen zu lösen, beginnt man mit dem aktuellen Zustand des Universums und verfolgt die Entwicklung in der Zeit zurück. Die genaue Lösung hängt insbesondere von den gemessenen Werten der Hubble-Konstante und verschiedener Dichteparameter ab, die den Massen- und Energiegehalt des Universums beschreiben. So stellt man fest, dass das Universum früher kleiner war. Gleichzeitig war es aber auch heißer und dichter. Formal führt die Lösung zu einem Zeitpunkt, an dem der Wert des Skalenfaktors verschwindet, d. h. das Universum keine Ausdehnung mehr hat und die Temperatur und Dichte unendlich groß werden. Dieser Zeitpunkt wird als “Urknall” bezeichnet. Er ist eine formale Singularität der Lösung der Friedmann-Gleichungen. Dies sagt jedoch nichts über die physikalische Realität einer solchen Anfangssingularität aus, denn die Gleichungen der klassischen Physik haben nur einen begrenzten Gültigkeitsbereich und sind nicht mehr anwendbar, wenn Quanteneffekte eine Rolle spielen, wie es im sehr frühen, heißen und dichten Universum angenommen wird. Eine Theorie der Quantengravitation ist erforderlich, um die Entwicklung des Universums in sehr frühen Zeiten zu beschreiben.

B. Die Zukunft des Universums

Die hellsten Sterne bestimmen die Helligkeit von Galaxien. In unserer Galaxie gibt es 100 Milliarden Sterne, von denen 90 Prozent kleiner als die Sonne sind, und 9 Prozent davon sind etwa so groß wie unsere Sonne und bis zu 2,5 Mal massereicher. Nur ein Prozent ist viel größer als die Sonne. Dieses eine Prozent der Sterne bestimmt jedoch die Helligkeit der Galaxie. Je größer ein Stern ist, desto verschwenderischer geht er mit seinem Kernbrennstoff um. Die hellsten Sterne leben nur einige zehn Millionen Jahre und explodieren am Ende ihres Lebens. Dabei reichern sie das interstellare Gas mit schweren Elementen an. Außerdem verdichten die Schockwellen der Explosion das Gas, so dass neue Sterne entstehen können. Durch diesen verschwenderischen Umgang mit Kernbrennstoff ist jedoch irgendwann kein Gas mehr für die Entstehung neuer Sterne vorhanden. Unsere Sonne enthält bereits 2 Prozent schwere Elemente, wobei der Anteil weiter zunimmt, so dass in einem Zeitraum von höchstens tausend Milliarden Jahren kein Gas mehr für die Bildung neuer Sterne zur Verfügung stehen wird. Unsere Galaxie wird dann schwach durch die kleineren Sterne leuchten, die viel länger leben als die Sonne. Die kleinsten von ihnen werden erst nach 1012-1013 Jahren erlöschen. Diese leuchten aber bereits so schwach, dass für unsere Augen – wenn es noch Menschen in ihrer jetzigen Form gibt – der Himmel fast sternenlos aussehen würde, da wir nur noch solche schwachen Sterne in der Nähe erkennen würden. In etwa 1013 Jahren wird das Universum langsam dunkel werden. Das Universum besteht dann nur noch aus langsam sterbenden Weißen Zwergen, Planeten, Pulsaren – den 20-Kilometer-Kernen von Riesensternen mit einer Dichte wie in einem Atomkern – und Schwarzen Löchern. Auch wenn es dunkel ist, sind die Gravitationskräfte der Sterne noch vorhanden. Sterne sind normalerweise weit voneinander entfernt. Die Erde ist acht Lichtminuten von der Sonne entfernt, und der nächste Stern ist 4,3 Lichtjahre entfernt. Eine sehr nahe Begegnung mit einem anderen Stern ist zwar unwahrscheinlich, reicht aber aus, um die Erde aus ihrer Umlaufbahn um die längst ausgebrannte Sonne zu werfen. In diesem Szenario wandert die Erde allein durch die Milchstraße. Dass ein Zusammentreffen mit einem massereichen Partner so nahe ist, dass es auch die Sonne betrifft, ist noch unwahrscheinlicher, aber selbst ein solches Ereignis sollte einmal in 1019 Jahren stattgefunden haben. Die Sonne fällt entweder näher an das galaktische Zentrum heran oder wird aus unserer Galaxie vertrieben. Sterne, die nicht aus unserer Galaxie verdrängt werden, fallen Sagittarius A* zum Opfer, dem Schwarzen Loch im Zentrum der Galaxie. Derzeit hat es eine Masse von 4,31±0,38106 Sonnenmassen, aber nach 1024 Jahren sind wahrscheinlich alle in dem System verbliebenen Sterne verschluckt worden. Nach dem heutigen Modell der Entstehung des Universums gehen wir davon aus, dass es aus einem Punkt, einer Singularität aller Masse, entstanden ist und sich seitdem weiter ausdehnt. Ob dies auch weiterhin der Fall sein wird, hängt davon ab, wie viel Materie sich im Universum befindet. Die Materie verlangsamt die Ausdehnung durch die Anziehungskraft der Schwerkraft. Wenn genügend Materie im Universum vorhanden ist, kann die Expansion schließlich zum Stillstand kommen und sich dann umkehren, so dass das Universum in einer Singularität endet. Das Universum wird weiter expandieren, wenn die Materie für dieses Szenario nicht ausreicht. Die dafür erforderliche Menge an Materie wird als kritische Dichte bezeichnet. Die Materie, die wir beobachten können (Sterne, Gaswolken), reicht dafür nicht aus, aber wir vermuten, dass es noch Materie geben könnte, die wir nicht sehen können, die so genannte dunkle Materie. Dabei könnte es sich um Elementarteilchen, schwarze Löcher oder verhinderte Sterne handeln, deren Masse nicht ausreichte, um den Kernbrennstoff zu zünden. Es gibt Hinweise auf erhebliche Mengen an dunkler Materie, da die Masse in Galaxienhaufen nicht ausreicht, um sie zusammenzuhalten. Nach der Relativitätstheorie stehen Raum und Zeit in Wechselwirkung mit Materie und Energie. Die Gravitation der Materie im Universum verlangsamt die kosmische Expansion. In der fernen Vergangenheit hätte die Expansionsrate größer sein müssen. Wenn die mittlere Dichte der Materie im Universum über einem bestimmten “kritischen” Wert liegt, dann sollte die Expansion sogar irgendwann zum Stillstand kommen und in eine Kontraktion übergehen. Diese kritische Dichte liegt bei etwa zwei bis drei Wasserstoffatomen pro Kubikmeter, was in etwa der Masse eines Sandkorns, verteilt auf das Volumen der Erde, entspricht. Die Beobachtungen zeigen jedoch, dass die Gesamtmasse der sichtbaren Materie – Gas, Sterne und Staub – höchstens für ein Prozent der kritischen Dichte ausreicht. Nach unserem heutigen Verständnis besteht die Hauptmasse des Universums aus dunkler Materie. Dunkel, weil sie sich nur durch die Schwerkraft in den Bewegungen der Sterne und Galaxien bemerkbar macht, aber nicht beobachtbar ist. Allerdings beträgt die Dichte nur etwa 30 Prozent der kritischen Grenze. Dafür spricht nun die Erforschung der Galaxienhaufen: ihre räumliche Verteilung und Dynamik, ihre zeitliche Entwicklung aufgrund von Beobachtungen und theoretischen Modellen sowie das Ausmaß von Gravitationslinseneffekten – Lichtablenkung entfernter Galaxien durch Vordergrundobjekte. Die durchschnittliche Dichte des Universums reicht also nicht aus, um seine Expansion zu stoppen. Dennoch haben Theoretiker lange Zeit ein Universum mit kritischer Dichte favorisiert, weil dies die einfachste Lösung ist, die am besten zur Hypothese der kosmischen Inflation passt. Die Hypothese der kosmischen Inflation besagt, dass sich das Universum in den ersten Sekundenbruchteilen nach dem Urknall exponentiell ausdehnen sollte, als es noch kleiner als ein Atom war – um den Faktor 1030. Auch das Muster der winzigen Temperaturschwankungen in der kosmischen Hintergrundstrahlung spricht für ein solches Universum mit kritischer Dichte. Sie ist der Nachhall des Urknalls und enthält subtile Informationen über die gesamten Eigenschaften des Universums. Die Dichte Ωtot ist durch Gl. 9 gegeben.

 

Ωtot=c (9)

 

wobei die mittlere Dichte und c die kritische Dichte ist, die ihrerseits durch Gleichung 10 definiert ist.

 

c=3H028πG≈8.5∙10-27kgm3 (10)

 

wobei H0 der aktuelle Hubble-Parameter ist, der die Expansionsrate des Universums angibt, und G die Gravitationskonstante ist. Ob die Masse ausreicht, um die Expansion des Universums zu stoppen, ist heute unbekannt. Die beobachtbare Masse macht nur 10-20 Prozent der kritischen Dichte aus.

Kritische Dichte >1: In diesem Fall kehrt sich die Expansion des Universums um, und das Universum wird in ferner Zukunft kollabieren. Für einen Beobachter wäre die Umkehrung der Expansion zunächst nicht erkennbar. Erst wenn nur noch eine Milliarde Jahre bis zum Kollaps verbleiben, bemerken Beobachter, dass der Himmel wieder heller wird. Es werden immer mehr Galaxien am Himmel erscheinen, da die Abstände zwischen den Galaxien kleiner werden. Um diese Zeit werden auch die Galaxienhaufen verschmelzen. Etwa 100×106 Jahre vor dem Kollaps verschmelzen die Galaxien, und Sterne werden nur noch in einer Gaswolke zu finden sein. Eine Million Jahre vor dem Kollaps wird die Temperatur im Weltraum auf Raumtemperatur ansteigen. Hunderttausend Jahre vor dem Kollaps wird der Nachthimmel so hell sein wie die Oberfläche der Sonne. Die Temperatur im Universum wird so stark ansteigen, dass die Planeten zu flüssigen Klumpen werden. Je weiter die Materie zusammengedrückt wird, desto schneller wachsen die schwarzen Löcher. Außerdem können Neutronensterne und Zwergsterne durch die Aufnahme von Materie neue Schwarze Löcher bilden. Zehn Jahre vor dem Kollaps verschmelzen sogar die schwarzen Löcher. Die Temperatur im Universum beträgt nun 10×106 Grad. Schließlich ist das Universum nur ein schwarzes Loch, so dass es keine Rolle spielt, ob es kollabiert, denn in einem schwarzen Loch gibt es weder Zeit noch Raum mehr. Ansonsten läuft jetzt alles rückwärts, wie beim Urknall: Neue Energie bildet spontan neue Teilchen, die Grundkräfte der Natur trennen sich, und alles endet in einer großen Singularität.

Kritische Dichte =0: Der langweiligste Fall. Wenn die Materiedichte genau den kritischen Wert hat, geht die Expansionsrate in unendlicher Zeit immer mehr gegen Null. Die Bedingungen in diesem Universum ähneln denen in einem Universum mit einem Omega von weniger als 1. Allerdings werden sich ein Elektron und ein Positron in astronomischen Abständen umkreisen. Sie kommen sich immer näher, bis sie sich schließlich gegenseitig vernichten und Photonen zurücklassen. Das Ende ist eine formlose Wüste aus Strahlung und Teilchen, die sich in der Ewigkeit verliert. Wenn nichts passiert, macht das Konzept der Zeit keinen Sinn mehr, und die Zeit hört auf zu existieren.

Kritische Dichte <1: Nach 1014 Jahren kommt die Wasserstofffusion zu höheren Elementen in den Sternen zum Stillstand. Sie erlöschen langsam, einer nach dem anderen. Das Universum besteht nur noch aus Planeten, Zwergsternen, Neutronensternen und Schwarzen Löchern. In 1017 Jahren wird sich auch die Lichtstrahlung des Restgases verlangsamen und auf die verbleibenden Sterne treffen. In 1026 Jahren senden Galaxien Gravitationsstrahlung aus. Die verbleibenden Sterne bewegen sich langsam spiralförmig in das Zentrum der Galaxie. Wenn die derzeitigen Theorien über die Entstehung des Universums zutreffen, müsste sich das Proton mit einer Halbwertszeit von 1032-1036 Jahren teilen. Einige Theorien, die eine Zerfallszeit von weniger als 1034 Jahren vorhersagen, können bereits ausgeschlossen werden, da bisher kein Protonenzerfall beobachtet werden konnte. Daher ist es unmöglich zu sagen, dass die Theorien, die eine längere Zerfallszeit vorhersagen, korrekt sind. Sollte dies der Fall sein, wäre die Hälfte der verbleibenden Materie im Universum nach 1036 Jahren in Positronen zerfallen. Spätestens nach 1039 Jahren wären demnach alle Protonen im Weltall zerfallen. Das wäre auch das Ende aller Atome, Moleküle, Planeten und anderer Himmelskörper, da die Atomkerne teilweise aus Protonen bestehen. Das Universum würde nur noch aus Licht, Elektronen, Positronen und schwarzen Löchern bestehen. Nach 1064-1067 Jahren beginnen die schwarzen Löcher langsam zu verdampfen. Die letzten und ehemals größten werden nach 10100 Jahren in einer Explosion enden. Ob Schwarze Löcher tatsächlich verdampfen, ist bisher nur eine Hypothese. Wenn das Proton nicht zerfällt, werden die Zwergsterne nach 101000 Jahren zu Neutronensternen. Nach 101026-101074 Jahren werden sich die Neutronensterne zu Schwarzen Löchern entwickelt haben, die dann verdampfen werden. Nach dieser Zeit wird das Universum nur noch aus Elementarteilchen bestehen.

Abb. 1. Krümmung des Universums in Abhängigkeit vom Dichteparameter [48]

Unabhängig von den möglichen Zukünften des Universums hat es nach menschlichen Maßstäben lange gedauert, bis der gegenwärtige Zustand des Universums erreicht wurde, und die Entwicklung wird noch lange weitergehen, bevor es zu seinem thermodynamischen Tod oder Zusammenbruch kommt. Daher ist eine Simulation des Universums oder von Teilen davon, die in Echtzeit abläuft, nicht sinnvoll, wenn wir erwarten zu erfahren, ob sich die Simulation wie das echte Universum verhält. Man sollte annehmen, dass man, wie bei den heutigen Computersimulationen, die Zeit beschleunigen kann, um schnellere Erkenntnisse zu gewinnen. Es stellt sich jedoch heraus, dass der Versuch, das Universum genau zu simulieren, einige Einschränkungen für die Simulationszeit mit sich bringt, wie in den folgenden Kapiteln erläutert wird.

VI. SIMULATION VON INNEN UND VON AUSSEN

Bevor wir die Simulation unseres Universums erörtern, müssen wir zwischen einer Simulation unseres aktuellen Universums und einem beliebigen Universum unterscheiden. Die Frage, ob es möglich wäre, bei einer exakten Simulation des von uns bewohnten Universums die Zukunft vorherzusagen, ist nicht nur interessant zu stellen, sondern auch wichtig zu beantworten, da sie uns an die ultimative Grenze der Berechenbarkeit führt, sowohl in Bezug auf die physikalischen Gesetze als auch auf die Komplexität. Wir unterscheiden zwischen der Simulation des Universums und der Simulation eines Universums. Ersteres bezieht sich auf die exakte Simulation des Universums, in dem wir leben (unser Universum), letzteres entweder auf einen Teil des Universums oder ein unspezifisches Universum, das auf denselben physikalischen Gesetzen wie das Universum beruhen kann oder auch nicht. Es werden eine Reihe von Annahmen über unser Verständnis der Entwicklung des Universums und alles darin getroffen, einschließlich astronomischer Objekte wie Planeten, Sterne, Nebel, Galaxien und Sternhaufen sowie dunkle Energie, dunkle Materie, das interstellare Medium, die Ausdehnung der Raumzeit und die Geometrie des Universums sowie die universellen Konstanten – die Lichtgeschwindigkeit im Vakuum, die Planck-Konstante, die Boltzmann-Konstante und die Gravitationskonstante, um nur einige zu nennen. Da unser heutiges Wissen über das Universum bei weitem nicht vollständig ist, werden für die nachfolgend vorgestellten Argumente einige Annahmen getroffen:

1. Wir (oder ein externer Programmierer) verstehen die physikalischen Gesetze, die die Evolution und die Zusammensetzung des Universums regeln, vollständig bis zur Ebene X. Dies beinhaltet ein vollständiges Verständnis der Kosmologie des Universums, einschließlich aller astronomischen Objekte, der Anfänge des Urknalls und der Inflation bis hin zur gesamten Materie – einschließlich der dunklen Materie -, der dunklen Energie und aller Gesetze auf der jeweiligen Skala, wie Relativität und Quantenphysik. Ein vollständiges Verständnis aller physikalischen Gesetze ermöglicht es uns (oder einem externen Programmierer), die Entwicklung des Universums in geeigneter Weise zu modellieren und Teile davon zu simulieren. Dies ermöglicht auch die Entstehung von Leben in der Simulation. Diese Annahme ist heute nicht mehr zutreffend.
2. Die Gesetze der Quantenphysik sind die grundlegendsten physikalischen Gesetze bis hinunter zur Ebene X. Die Beschränkungen, die die Quantenphysik der Gewissheit auferlegt, bestimmen, wie genau wir in unserem Universum messen können. Die Planck-Einheiten sind die zugänglichen Grenzen von Zeit, Raum, Masse und Temperatur, über die hinaus kein physikalisches Gesetz Bedeutung hat. Es gibt wissenschaftlich fundierte Experimente und starke Anzeichen dafür, dass dies zutrifft, aber es bleiben viele Fragen offen, z. B. wie sich die Quantenphysik mit der allgemeinen Relativitätstheorie vereinbaren lässt. Daher ist diese Annahme heute nur teilweise zutreffend.
3. Ein externer Programmierer kann beschließen, ein Universum zu simulieren, in dem dieselben physikalischen Gesetze gelten wie in seinem Universum, oder die Simulation auf andere physikalische Gesetze stützen. Wenn wir als externer Programmierer die Absicht haben, Hinweise darauf zu finden, ob wir an einer Simulationskette teilnehmen, scheint es vernünftig, die Simulation auf dieselben physikalischen Gesetze zu stützen, die in dem Universum herrschen. Ein externer Programmierer des Universums kann ebenfalls nicht wissen, ob er an einer Simulationskette teilnimmt, und wir gehen davon aus, dass ein externer Programmierer ebenfalls Anhaltspunkte dafür finden möchte, ob es wahr ist oder nicht, und eine Simulation eines Universums auf die gleichen physikalischen Gesetze stützen würde, die er in seinem Universum beobachtet. Da wir über die Simulation eines Universums nachdenken, wird die Frage, ob das (unser) Universum auf denselben physikalischen Gesetzen beruht wie das Universum eines potenziellen externen Programmierers, irrelevant: Wenn wir als externe Programmierer agieren und unserer Simulation dieselben physikalischen Gesetze zugrunde legen wie unserem Universum, und wenn eine Simulationskette entsteht, in der nachfolgende externe Programmierer ihren Simulationen ebenfalls dieselben physikalischen Gesetze zugrunde legen, dann sind die Handlungen dieser externen Programmierer Kandidaten für Beobachtungen, nach denen man im Universum suchen kann, unabhängig davon, ob letzteres auf denselben physikalischen Gesetzen wie das Universum eines potenziellen externen Programmierers beruht.

Die Ebene X bezieht sich auf die tiefste physikalische Strukturebene der Materie und die physikalischen Gesetze, die auf dieser Ebene gelten. Eine der Hypothesen der Stringtheorie besagt, dass Quarks – die Bestandteile von Hadronen, einschließlich Protonen und Neutronen – und Elektronen aus noch kleineren vibrierenden Energieschleifen bestehen, die Strings genannt werden, und dass dies die grundlegendsten Elemente sind, aus denen alle Materie besteht. Es wird von entscheidender Bedeutung sein zu verstehen, ob X auch die Granularitätsebene ist, auf der eine “ausreichend gute” Simulation beruhen muss, da beispielsweise die Funktionsweise eines makroskopischen Motors nicht allzu sehr vom Verhalten einzelner Quarks beeinflusst zu werden scheint.

Außerdem muss zwischen Simulation und Emulation unterschieden werden. Äußerlich verhält sich eine Emulation des Universums genauso wie das reale Universum, aber die internen Zustände der Emulation müssen nicht mit denen des realen Universums identisch sein. So muss eine Emulation beispielsweise nicht dieselben physikalischen Gesetze und Verhaltensweisen auf unbeobachteten Skalen, d. h. bis hinunter zur Ebene X, berücksichtigen, solange sie sich auf den gewünschten beobachteten Skalen genau wie das Universum verhält. Andererseits repräsentiert eine Simulation des Universums in ihrem internen Zustand alle physikalischen Gesetze und Zustände der simulierten Bestandteile genau so, wie sie außerhalb der Simulation sind. Sowohl die Simulation als auch die Nachbildung des Universums können überzeugende Ergebnisse liefern. Eine Simulation bildet jedoch die Grundlage für die weitere Diskussion, da nicht nur das Verhalten nachgeahmt, sondern auch Teile des Universums reproduziert werden sollen, so dass die Simulation sowohl intern als auch extern vom realen Universum physisch nicht zu unterscheiden ist.

A. Simulation des Universums

Die Durchführbarkeit einer Simulation des Universums, genauer gesagt einer exakten Simulation des von uns bewohnten Universums in voller Größe und Komplexität, die es uns ermöglichen würde, künftige Ereignisse vorherzusagen und beliebige Zustände in der Zeit rückwärts exakt zu simulieren, kann selbst unter den oben genannten Annahmen logischerweise ausgeschlossen werden. Mehrere Beschränkungen der Berechenbarkeit verhindern die Erstellung einer solchen Simulation. Wenn das Universum exakt simuliert werden soll, muss die Simulation auch den für die Simulation verwendeten Computer umfassen, den wir als “Simulation von innen” bezeichnen. Bei der “Simulation von außen” hingegen ist der interne Zustand des Computers, der für die Simulation des Universums verwendet wird, vom Zustand des Universums entkoppelt.

• Jede Simulation erfolgt in diskreten Zeitschritten und wird einen Zeitschritt nach dem anderen vorhersagen, bis die gewünschte Vorhersagezeit erreicht ist. Nehmen wir an, die Simulation beginnt zum Zeitpunkt t0 mit der Erwartung, t1 zu simulieren, um den Zustand des Universums zum Zeitpunkt t1 vorherzusagen, und die Rechenzeit tc, um dies durchzuführen, ist kleiner als t1 (siehe Gleichung 11).

 

t0=t1-tc (11)

Wenn der Computer den Zustand des Universums zum Zeitpunkt t1 in tc vorausgesagt hat, hat er auch seinen internen Zustand zum Zeitpunkt t1 vorausgesagt. Wird der Computer gebeten, den Zustand des Universums zum Zeitpunkt t2 vorherzusagen, so wird er seine Vorhersagen auf den Zustand des Universums, einschließlich seiner internen Konfiguration zum Zeitpunkt t1, stützen. Da jedoch tc<t1 ist, würde der Computer beginnen, seine interne Konfiguration zu ändern, um den Zustand des Universums bei t2 vorherzusagen, bevor t1 erreicht ist, und seine ursprünglichen Vorhersagen über seinen internen Zustand bei t1 sind nicht korrekt, wenn t1 erreicht ist. Egal wie klein die Zeitschritte sind, solange tc kleiner als t1 ist, tritt dieses Problem auf, was zu der Schlussfolgerung führt, dass ein Computer innerhalb des Universums nicht dazu verwendet werden kann, das Universum zu simulieren; er kann nur ein Universum simulieren, entsprechend unserer zuvor gemachten Definitionen. Der Kern dieses Arguments ist, dass eine Simulation des Universums nicht schneller laufen kann als die Echtzeitentwicklung des Universums und dass die Zukunft des Universums nicht vorhergesagt werden kann, wenn die Vorhersage exakt sein soll. Denn der Computer wird immer seinen eigenen falschen internen Zustand vorhersagen, solange tc<t1 ist. Wenn tc=t1 und keine anderen Einschränkungen gegeben sind, würde die Simulation korrekte Ergebnisse liefern, aber in Echtzeit ablaufen. Im Folgenden nennen wir dies die Einschränkung der rechnerischen Vorhersagbarkeit.

• Der erste Grund für die Unberechenbarkeit der Simulation von innen heraus ist, dass – unter der Annahme, dass es möglich wäre, eine Simulation von innen heraus durchzuführen, einschließlich einer korrekten Darstellung des internen Zustands des Computers zu einem bestimmten Zeitpunkt – jeder simulierte Computer auch das Universum einschließlich sich selbst simulieren müsste, was eine Rekursion darstellt. Die Rekursion ist nicht nur rechenintensiv, sondern führt auch zu einer generellen Unberechenbarkeit der Simulation, da die verfügbaren Rechenressourcen, wie Speicher und Recheneinheiten, zur Berechnung einer Reihe von Simulationen S={s1,…,sn} mit n→∞ verwendet werden müssen. Anstelle der Rechenressourcen, die für die Simulation des Universums im Inneren benötigt werden, benötigt jeder simulierte Computer die Rechenressourcen, um sich selbst und das Universum zu simulieren, was bedeutet, dass der Computer in s1 das Universum und sich selbst von innen und unendlich oft von außen simulieren muss, was nicht machbar und somit unmöglich ist. Entweder würden dem Computer in s1 irgendwann die Ressourcen ausgehen, oder die Rechenressourcen in sn würden nicht ausreichen, um eine weitere Simulation sn+1 durchzuführen. Dieses Argument wird im Folgenden als erste Berechnbarkeitsbeschränkung bezeichnet.
• Ein weiterer Grund für die Unberechenbarkeit der Simulation von innen heraus ist die Komplexität des Universums. Wir sind daran gewöhnt, dass Computer uns über Virtual-Reality-Geräte oder Bildschirme Zugang zu virtuellen Welten verschaffen, und die virtuellen Welten der Videospiele und des Metaversums sind immer komplexer geworden, obwohl die Informationsverarbeitung auf rein klassischen Computern stattfindet, die nicht einmal enorm leistungsstark sein müssen. Mit Hilfe von Algorithmen können Umgebungen erzeugt und die Unendlichkeit zufällig und dynamisch nachgeahmt werden. Dies ist jedoch irreführend, wenn es um die Simulation des Universums von innen heraus geht, da ein Computer, der eine solche Simulation durchführt, alle Teilchen des Universums, von denen wir derzeit 1078-1082 annehmen, in seinem internen Zustand darstellen müsste. Eine grundlegende Frage ist, ob das kodierende Objekt einfacher sein kann als das kodierte Objekt. Die fortschrittlichsten Quantencomputer von heute verwenden Quantenobjekte, um Zustände anderer Systeme zu kodieren, sind aber auf binäre Zustände beschränkt. Ein solcher Quantencomputer kann beispielsweise die Energieniveaus von Atomen verwenden, um binäre Zustände zu kodieren – den Grundzustand zur Kodierung von 0 und einen angeregten Zustand zur Kodierung von 1. Ein Bit, egal ob es sich um ein Quantenbit oder ein klassisches Bit handelt, ist die kleinste Informationseinheit, und ein physikalisches System, das die Information eines Bits aufnehmen kann, ist das grundlegendste System zur Speicherung von Informationen. Wie viele Bits werden benötigt, um ein Atom vollständig zu beschreiben? Ein Atom selbst ist viel komplexer als ein System mit zwei Zuständen. Zum Beispiel befinden sich die Elektronen in Wahrscheinlichkeitswolken um die Atomkerne, den so genannten Orbitalen (Abb. 2).

Abb. 2. Einige elektronische Orbitale. Ein Orbital ist eine Wahrscheinlichkeitswolke, die die Position eines Elektrons innerhalb eines Atoms bestimmt [49].

Jedes Elektron in einem Atom wird durch vier verschiedene Quantenzahlen beschrieben, die Informationen über das Energieniveau oder den Abstand des Elektrons vom Kern, die Form der Orbitale, die Anzahl und Ausrichtung der Orbitale und die Richtung des elektronischen Spins liefern. Diese vier Quantenzahlen enthalten vollständige Informationen über die Bahnen und die Bewegung jedes Elektrons innerhalb eines Atoms. Alle Quantenzahlen aller Elektronen zusammen werden durch eine Wellenfunktion beschrieben, die der Schrödinger-Gleichung entspricht. Die Schrödinger-Gleichung ist einfach zu verstehen, aber selbst die leistungsfähigsten Quantencomputer der Zukunft werden viel mehr Atome benötigen, um die Zustände eines Systems zu kodieren, als das zu simulierende System umfasst. Das Wasserstoffatom zum Beispiel besteht aus einem Elektron und einem Proton. Beide Teilchen bewegen sich um einen gemeinsamen Massenschwerpunkt, und diese interne Bewegung ist äquivalent zur Bewegung eines einzelnen Teilchens mit reduzierter Masse. r ist der Vektor, der die Position des Elektrons des reduzierten Teilchens relativ zur Position seines Protons angibt. Die Ausrichtung des Vektors, der vom Proton zum Elektron zeigt, gibt die Richtung von r an, und seine Länge ist der Abstand zwischen den beiden. In den heutigen Simulationen werden Näherungen gemacht, z. B. dass die reduzierte Masse gleich der Masse des Elektrons ist und dass sich das Proton im Zentrum der Masse befindet. Gl. 12 ist die Schrödinger-Gleichung für das Wasserstoffatom, wobei E die Energie des Systems angibt.

 

Hr,θ,ϕψ(r,θ,ϕ)=Eψ(r,θ,ϕ) (12)

 

Die zeitliche Entwicklung eines Quantenzustands ist einheitlich, und eine einheitliche Transformation kann als eine Rotation im Hilbert-Raum betrachtet werden. Die Entwicklung erfolgt über einen speziellen selbstadjungierten Operator, den Hamiltonian H des Systems. Die Gleichung ist in Kugelkoordinaten gegeben, wobei r den Radius bestimmt und 0≤<2 der Azimut und 0≤ der Polarwinkel ist. Die zeitunabhängige Schrödinger-Gleichung für ein Elektron um ein Proton in Kugelkoordinaten ist dann gegeben durch Gl. 13.

 

-22μr2∂rr2∂r+1sin ∂θsin(θ∂θ+1 22 -e24π0rr,θ,ϕ=Eψ(r,θ,ϕ) (13)

 

In Gl. 13 ist die reduzierte Plancksche Konstante, der Term in den eckigen Klammern beschreibt die kinetische Energie, und der Term, der von der kinetischen Energie abgezogen wird, ist die potenzielle Coulomb-Energie. (r,,) ist die Wellenfunktion des Teilchens, 0 die Dielektrizitätskonstante des freien Raums und die reduzierte Zweikörpermasse des Wasserstoffkerns der Masse mp und des Elektrons der Masse mq (Gl. 14).

 

μ=mqmpmq+mp (14)

 

Es ist möglich, die Variablen in Gl. 13 zu trennen, da der Drehimpulsoperator die radiale Variable r nicht einbezieht, was mit Hilfe einer Produktwellenfunktion geschehen kann. Eine gute Wahl ist Gl. 15, da die Eigenfunktionen des Drehimpulsoperators sphärische harmonische Funktionen Y(θ,ϕ) sind [50,51].

 

ψ(r,θ,ϕ)=R(r)Y(θ,ϕ) (15)

 

Die Radialfunktion R(r) beschreibt den Abstand des Elektrons vom Proton, und Y(,) gibt Auskunft über die Position im Orbital, und eine Lösung für beide mit En hängt nur von der primären Quantenzahl n ab (Gl. 16).

 

En=mee48e02h2n2 (16)

 

Die Wellenfunktionen des Atoms (r,,) sind die zuvor besprochenen Atomorbitale, und jedes der Orbitale beschreibt ein Elektron in einem Atom. Betrachtet man nur bestimmte Orbitale in einem Atom, z. B. von 1s bis 5g, so müsste das zur Kodierung verwendete System 6,8 Bits verwenden können, was sich aus dem Logarithmus zur Basis 2 von 110 ergibt (Gl. 17). Nach der Quantentheorie gibt es eine unendliche Anzahl von Kombinationen dieser vier Quantenzahlen pro Atom, so dass das Kodierungssystem eine unendliche Anzahl von Kodierungssystemen verwenden müsste. Außerdem kann die Schrödingergleichung bis heute nur für die einfachsten Systeme, wie wasserstoffähnliche Atome, gelöst werden. Diese Einschränkung ist kein Hindernis für Computer, da auch Quantencomputer nicht in der Lage sein werden, die Schrödinger-Gleichung für große Systeme analytisch zu lösen. Allerdings werden Quantencomputer bei der numerischen Lösung der Gleichung einen Geschwindigkeitsvorteil bieten. Daher scheint die Annahme vernünftig, dass zur Verschlüsselung der vollen Komplexität eines Quantensystems ein identisches Quantensystem erforderlich ist.

 

110=6.8 (17)

 

Um dieses Kunststück zu vollbringen, müsste der Computer, wenn er den gleichen physikalischen Gesetzen unterliegt wie die Simulation, mindestens aus der gleichen Anzahl von Teilchen bestehen und so groß sein wie das Universum. “Mindestens” deshalb, weil die Objekte, die der Computer verwendet, um die Objekte des Universums zu kodieren, die gleiche Repräsentationskraft haben müssten, was unmöglich ist und somit die Unberechenbarkeit der Simulation von innen heraus beweist. Es wurde festgestellt, dass es einen starken Zusammenhang zwischen der ultimativen Informationskapazität von Geräten und dem verallgemeinerten zweiten Hauptsatz der Thermodynamik (GSL) gibt [52]. Es wurde gezeigt, dass die Gesamtfläche der Ereignishorizonte in Schwarzen Löchern bei bestimmten Ereignissen wie der Verschmelzung von Schwarzen Löchern niemals abnimmt [53]. Die GSL besagt, dass jedes Mal, wenn Materie in ein Schwarzes Loch fällt, die Zunahme der Entropie des Schwarzen Lochs den Verlust der Entropie der Materie (über)kompensiert und verhindert, dass sowohl die Entropie außerhalb eines Schwarzen Lochs als auch die Entropie des Schwarzen Lochs abnimmt. Es wurde ferner theoretisch bestimmt, dass die Proportionalitätskonstante zwischen der Entropie des Schwarzen Lochs und der Fläche des Ereignishorizonts des Schwarzen Lochs ein Viertel der Fläche des Ereignishorizonts in Planck-Flächen beträgt (Gl. 18) [52,54], wobei eine Planck-Fläche der Planck-Länge von 10-33 cm zum Quadrat entspricht, was für ein Schwarzes Loch mit einem Durchmesser von einem Zentimeter eine informationstheoretische Entropie [55] von 1066 Bit ergeben würde. Die Entropie, wie sie in der Informationstheorie definiert ist (Gl. 20), unterscheidet sich von der thermodynamischen Entropie (Gl. 19), auf die in dieser Veröffentlichung bereits eingegangen wurde, insbesondere in der Art und Weise, wie sie berechnet wird. In den Gleichungen 18, 19 und 20 ist S die thermodynamische Entropie, H die informationstheoretische Entropie, kB die Boltzmann-Konstante, lp2 die Planck-Länge, W die thermodynamische Wahrscheinlichkeit, die die Anzahl der alternativen mikroskopischen Anordnungen definiert, die demselben makroskopischen Zustand entsprechen, und X eine diskrete Zufallsvariable, die Werte in.

 

SBH=kBA4lp2 (18)

 

S=kBln W (19)

 

x∈χpxp(x) (20)

 

Mit der GSL lassen sich Grenzen für die Informationsspeicherkapazität eines beliebigen isolierten Systems setzen, und bahnbrechende Arbeiten über die holographische Schranke [56-59] brachten ans Licht, dass die maximal mögliche Entropie eines Systems nicht von seinem Volumen, sondern von seiner Grenzfläche oder Oberfläche abhängt. Für ein bestimmtes Raumvolumen begrenzt die holografische Grenze, wie viel Entropie in Energie und Materie enthalten sein kann. Der überraschende Zusammenhang zwischen Entropie und der Oberfläche eines Schwarzen Lochs sowie die enorme Informationsmenge, die theoretisch auf der Oberfläche eines kleinen Schwarzen Lochs gespeichert werden kann, zeigt, dass selbst räumlich kleine theoretische Informationsverarbeitungsgeräte riesige Datenmengen speichern können, beispielsweise 1066 Bit für ein Schwarzes Loch mit einem Durchmesser von einem Zentimeter. Wollte man jedoch das Universum mit all seinen Objekten simulieren, müssten sicherlich auch Schwarze Löcher simuliert werden, die das Verhalten von Galaxien und indirekt auch von Strukturen jenseits davon bestimmen. Das Argument, dass ein sehr leistungsfähiges, aber kleines Informationsverarbeitungsgerät zur Simulation des Universums verwendet werden könnte, ist nicht stichhaltig. Diese Ergebnisse liefern jedoch starke Hinweise darauf, dass ein Gerät, das ein Universum simuliert, nicht nur nicht die Größe eines Universums haben muss, sondern viel kleiner sein kann, als es mit unseren modernsten Informationsverarbeitungsgeräten derzeit vorstellbar ist. Von nun an wird dieses Argument als zweite Berechnbarkeitsbeschränkung bezeichnet.

• Wenn schließlich die Quantenphysik die grundlegendsten physikalischen Gesetze umfasst, wovon wir derzeit ausgehen, dann setzt sie der Genauigkeit unseres Wissens über Teilchen gewisse Grenzen. Obwohl die Quantenphysik die grundlegenden Theorien zur Beschreibung des Universums umfasst, unterscheidet sich die konzeptionelle Struktur dieser Theorien grundlegend von der der klassischen Physik – der Physik, die wir jeden Tag erleben, wenn wir mit Teilen des Universums interagieren. Die Aussagen der Quantenphysik über das Universum sind Aussagen über die Ergebnisse von Messungen. Im Gegensatz zur klassischen Physik können wir in jedem Fall probabilistische Aussagen machen; zum Beispiel kann man die Werteverteilung nur vorhersagen, wenn man ein Ensemble ähnlicher Systeme misst. Die Heisenbergsche Unschärferelation (Gl. 21) ergibt sich aus der Tatsache, dass ein physikalisches System quantenphysikalisch mit Hilfe einer Wellenfunktion beschrieben wird.

 

x×p≈h (21)

 

Die quantenphysikalische Unschärfe entsteht in allen wellenartigen Systemen aufgrund der Materie-Wellen-Natur aller Quantenobjekte. Zum Beispiel hängt ∆x des Ortes eines Photons von der Wellenlänge des betrachteten Lichts ab. Andererseits wirkt die Ablenkung des Lichtquants wie ein Stoß auf das Teilchen, wodurch der Impuls des Körpers eine Unbestimmtheit von ∆p erfährt, bekannt als Compton-Streuung. Als grundlegende untere Grenze für diese Unsicherheiten schätzte Heisenberg mit Hilfe der de Broglie-Beziehung [60], dass das Produkt aus ∆x und ∆p nicht kleiner sein kann als das der für die Quantenphysik charakteristischen Naturkonstante, der Planckschen Konstante h. Heisenberg formulierte diese fundamentale Grenze der Messbarkeit in der in Gl. 21 gegebenen Aussage. Während in der klassischen Mechanik Ort und Impuls einfache Größen sind, die im Prinzip genau gemessen werden können, ergeben sich ihre Verteilungen in der Quantenmechanik als Quadrat des Absolutwerts der Wellenfunktion oder ihrer Fouriertransformation. Das heißt, sie können nicht unabhängig voneinander bestimmt werden. Da die Verteilungen von Ort und Impuls von der Wellenfunktion des Systems abhängen, hängen auch die Standardabweichungen der Messungen voneinander ab. Je genauer man den Ort eines Teilchens in der üblichen quantenmechanischen Beschreibung bestimmen will, desto größer ist die Ungenauigkeit des Impulses – und andersherum. Wenn die Quantenphysik die grundlegendsten physikalischen Gesetze ist – sozusagen die Maschinensprache des Universums -, dann verhindert die Unschärferelation, dass wir eine genaue Simulation des Universums von innen und außen erstellen können. Darüber hinaus hindert uns die Verschränkung auch daran, das Universum von innen zu simulieren, da es keine Möglichkeit gibt, die Teilchen, aus denen der für die Simulation verwendete Computer besteht, von den Teilchen des Universums zu trennen. Von Verschränkung spricht man in der Quantenphysik, wenn ein zusammengesetztes physikalisches System, z. B. ein System, das aus mehreren Teilchen besteht, als Ganzes betrachtet einen wohldefinierten Zustand annimmt, ohne jedem Teilsystem einen wohldefinierten Zustand zuordnen zu können. Dieses Phänomen gibt es in der klassischen Physik nicht. Dort sind zusammengesetzte Systeme immer trennbar. Jedes Teilsystem hat zu jedem Zeitpunkt einen bestimmten Zustand, der sein jeweiliges Verhalten bestimmt, wobei die Gesamtheit der Zustände der einzelnen Teilsysteme und deren Wechselwirkung das Verhalten des Gesamtsystems vollständig erklären. In einem quantenphysikalisch verschränkten Zustand des Systems hingegen nehmen die Teilsysteme mehrere ihrer möglichen Zustände gleichzeitig an, wobei jedem dieser Teilsystemzustände ein anderer Zustand der anderen Teilsysteme zugeordnet ist. Um das Verhalten des Gesamtsystems richtig zu erklären, muss man alle diese koexistierenden Möglichkeiten zusammen betrachten. Wenn jedoch eine Messung an jedem Teilsystem durchgeführt wird, wird nur eine dieser Möglichkeiten beobachtet, wobei die Wahrscheinlichkeit, dieses bestimmte Ergebnis zu messen, für alle Ergebnisse durch eine Wahrscheinlichkeitsverteilung bestimmt ist. Die Messergebnisse von mehreren verschränkten Teilsystemen sind miteinander korreliert. Das heißt, je nach Messergebnis eines Teilsystems ergibt sich eine andere Wahrscheinlichkeitsverteilung für die möglichen Messergebnisse der anderen Teilsysteme. Verschränkte Zustände sind häufig; ein verschränkter Zustand entsteht immer dann, wenn zwei Teilsysteme miteinander interagieren, z. B. miteinander kollidieren, mit unterschiedlichen, aber aufeinander abgestimmten Möglichkeiten, wie sie sich weiter verhalten, z. B. in welche Richtung sie sich nach dem Zusammenstoß weiter ausbreiten. Nach der Quantenphysik sind alle diese Möglichkeiten mit einer bestimmten Wahrscheinlichkeit verbunden, mit der sie bis zum Zeitpunkt der quantenmechanischen Messung entsprechend koordiniert im Zustand des Gesamtsystems repräsentiert sein müssen. Die Verschränkung wird zerstört, sobald eines der Teilsysteme auf einen seiner Zustände fixiert ist. Dann geht ein anderes Teilsystem, das durch die Verschränkung mit dem ersten Teilsystem verbunden ist, sofort in den Zustand über, der dem durch Beobachtung ermittelten Zustand des ersten Teilsystems zugeordnet ist. Der Zustand des Gesamtsystems weist dann keine Verschränkung mehr auf, da sich beide Teilsysteme nun in ihrem spezifischen Zustand befinden. Viele Experimente haben die durch Verschränkung verursachten Korrelationen nachgewiesen. Diese Korrelationen sind unabhängig von der Entfernung zwischen den Orten, an denen die Messungen an den Teilsystemen vorgenommen werden, und dem Zeitabstand zwischen den Messungen. Das Gleiche gilt, wenn die Messungen so weit voneinander entfernt sind und so schnell nacheinander oder sogar gleichzeitig durchgeführt werden, dass das Messergebnis des einen Teilchens den Zustand des anderen in keiner Weise physikalisch beeinflusst haben kann. Bei bestimmten Experimenten sind die Korrelationen so stark, dass sie im Prinzip durch keine Theorie erklärt werden können, die wie die klassische Physik auf dem physikalischen Prinzip des lokalen Realismus beruht. Der lokale Realismus besagt, dass jedes Teilsystem immer einen wohldefinierten Zustand hat, auf den ein anderes, räumlich entferntes Teilsystem nur mit Lichtgeschwindigkeit einwirken kann. Nach dem Bell’schen Theorem ist es auch ausgeschlossen, dass eine solche lokal-realistische Theorie mit hypothetischen zusätzlichen verborgenen Variablen das Phänomen der Quantenkorrelation beschreiben könnte. In der Wissenschaft wird immer noch darüber diskutiert, ob die Unvereinbarkeit der Quantenphysik mit lokalen Theorien mit verborgenen Variablen und die probabilistische Natur der Teilchen ausreichen, um ein deterministisches Universum auszuschließen, und ob dies einen freien Willen ermöglichen würde [61-63]. Wenn man die Perspektive eines internen oder externen Programmierers im Sinne dieser Publikation annimmt, würde der Programmierer, um eine genaue Vorhersage über zukünftige Zustände eines Universums machen zu können (andere Beschränkungen beiseite gelassen), ein perfektes Messgerät haben wollen – ein Gerät, das von seiner Umgebung völlig isoliert ist (und somit nicht von seiner Umgebung beeinflusst wird) und es ihm ermöglicht, Quantenzustände zu untersuchen. In einer Simulation muss ein Teilchen in voller Komplexität im internen Zustand des Computers existieren, der es simuliert. Computer mit solchen Fähigkeiten gibt es heute nicht, und die heutigen Quantencomputer sind nicht in der Lage, komplexe Quantenphysik oder -chemie zu simulieren. Angenommen, es gibt einen solchen Computer und ein solches Messgerät, dann hat ein Programmierer mehrere Möglichkeiten:

• Er könnte zwei identische Simulationen, s1 und s2, parallel laufen lassen, und sobald beide Simulationen einen bestimmten Zeitpunkt tx erreicht haben, könnte er s2 so beschleunigen, dass es, sagen wir, tx+2 erreicht, bevor s1 dort ankommt, und in s2 hineinspitzen, um den zukünftigen Zustand tx+2 von s1 zu erfahren. Der Programmierer wäre jedoch überrascht zu erfahren, dass die Universen bereits bei tx nicht mehr identisch sind, da jede quantenphysikalische Wechselwirkung zwischen Teilchen probabilistisch ist. Selbst wenn die Anfangskonfiguration von s1 und s2 identisch ist – was denkbar ist -, kann die Entwicklung der beiden Universen ähnlich, aber nicht identisch sein. So hängt beispielsweise das Ergebnis chemischer Reaktionen von Quanteneffekten wie dem Elektronenspin ab. Außerdem kollabieren die Wellenfunktionen von Systemen und die Verschränkung und Entschränkung zwischen Teilchen ständig, und das Ergebnis ist nicht deterministisch. Zwei identische Wechselwirkungen in s1 und s2 können zu unterschiedlichen Ergebnissen führen. Im Laufe zahlloser Wechselwirkungen wird dies zu unterscheidbaren/unterschiedlichen makroskopischen Zuständen führen.
• Der Programmierer kann einfach eine Simulation s1 laufen lassen und beschließen, bei tx einen “Schnappschuss” davon zu machen, und diesen Schnappschuss, bevor er tx+2 erreicht, in einen anderen Computer einspeisen, um den Zustand der Simulation bei tx+2 vorherzusagen. Es ist nicht möglich, einen Schnappschuss zu erstellen, der den vollständigen Quantenzustand aller Teilchen zum Zeitpunkt tx enthält, denn in der Quantenphysik hindert das No-Cloning-Theorem [64-66] den Programmierer daran, dies zu tun. Kurz gesagt, es beweist die Unmöglichkeit, eine unabhängige und identische Kopie eines beliebigen unbekannten Quantenzustands zu erstellen.
• Der Programmierer könnte jeden Quantenzustand der Simulation mit seinem perfekten Messgerät bei tx untersuchen, klassische Ergebnisse erhalten und diese dazu verwenden, neue Quantenzustände in einem anderen Computer zu erzeugen, um den Zustand der Simulation bei tx+2 vorherzusagen. Die Herausforderung besteht darin, dass jedes noch so gute Messgerät mit einem Quantenzustand in Wechselwirkung treten muss, was zu einer Zustandsänderung eben dieses Quantenzustands führt, bevor er kollabiert (ein Messgerät bewirkt immer den Kollaps der informationsreichen, aber unzugänglichen Überlagerung eines Zustands auf einen bestimmten Zustand). Ein Beispiel ist die Wechselwirkung eines Photons mit einem Elektron, um dessen Spin zu untersuchen. Außerdem ist es unmöglich, ein Quantensystem vollständig von seiner Umgebung zu isolieren [67]. So kann auch ein Messgerät, das aus vielen Quantensystemen besteht, nicht von seiner Umgebung oder seinen eigenen irrelevanten physikalischen Eigenschaften isoliert werden. Folglich ist es, selbst wenn ein Messgerät so gut wie möglich wird, unmöglich, mit diesem Ansatz zukünftige Zustände vorherzusagen.
• Der Programmierer kann eine Simulation mit einem Computer durchführen, der Quantenzustände simuliert, ohne Quanteneffekte für die Berechnung zu nutzen, entsprechend den Überlegungen zu simulierten Quantencomputern [41, 68]. Da die Anzahl der Quantenzustände, selbst für einzelne Teilchen, unendlich ist, kann ein solcher Computer nur ungefähre Simulationen erstellen, und die für die Simulation selbst einfacher Systeme erforderliche Rechenleistung würde mit dem Grad der Genauigkeit steigen. Die dritte hier skizzierte Bedingung für die Berechenbarkeit würde sogar noch früher erfüllt werden.

Ob das Universum nicht-deterministisch ist, ist Gegenstand intensiver Debatten, und zu den Argumenten für Determinismus gehören der Superdeterminismus [61,69] und die deterministische Quantenmechanik [70]. Die deterministische Quantenmechanik argumentiert unter anderem mit ontologischen Basen, bei denen die Schrödinger-Gleichung Basiszustände zu hinreichend dichten Zeitpunkten in andere Basiszustände schickt, und dass die in der Quantenmechanik verwendeten überlagerten Zustände nicht experimentell erzeugt werden können [70], sondern als solche geschrieben werden, weil uns das Wissen zur Beschreibung des genauen ontologischen Zustands fehlt. Dies wird noch nicht durch Theorie oder Experiment gestützt, da die ontologischen Grundlagen noch nicht gefunden wurden.

Superdeterminismus ist eine hypothetische Klasse von Theorien, die dem Bell’schen Theorem entgehen, weil sie vollständig deterministisch sind. Das Bellsche Theorem geht davon aus, dass die Art der Messungen an jedem Detektor unabhängig von der zu messenden verborgenen Variable gewählt werden kann. Damit das Argument der Bellschen Ungleichung Bestand hat, muss es möglich sein, über das Ergebnis des Experiments zu sprechen, wenn andere Entscheidungen getroffen worden wären. In einer deterministischen Theorie sind die Messungen, die die Experimentatoren an jedem Detektor auswählen, durch die physikalischen Gesetze vorgegeben. Es kann argumentiert werden, dass es falsch ist, darüber zu sprechen, was passiert wäre, wenn andere Messungen gewählt worden wären: eine andere Wahl der Messungen war physikalisch nicht möglich. Da die gewählten Messungen im Voraus festgelegt sind, können die Ergebnisse an einem Detektor durch die Art der Messung an einem anderen Detektor beeinflusst werden, ohne dass die Informationen schneller als mit Lichtgeschwindigkeit übertragen werden müssen. Es gibt eine Möglichkeit, der Schlussfolgerung der Überlichtgeschwindigkeit und der Fernwirkung durch Verschränkung zu entgehen, aber sie setzt absoluten Determinismus im Universum voraus, das völlige Fehlen eines freien Willens. Wenn wir davon ausgehen, dass die Welt superdeterministisch ist, was bedeutet, dass nicht nur die unbelebte Welt, sondern auch unser eigenes Verhalten vorherbestimmt ist, einschließlich unseres Glaubens, dass wir frei sind, eine Erfahrung einer anderen vorzuziehen, dann ist auch die Entscheidung, welche Messungen ein Experimentator vornimmt, vorherbestimmt, und alle Schwierigkeiten verschwinden. Diesem Argument folgend besteht kein Bedarf an superluminöser Kommunikation. Wie bei jedem Signal ist es sinnlos, Teilchen A mitzuteilen, welche Messung an Teilchen B vorgenommen wurde, da das Universum, einschließlich Teilchen A, bereits “weiß”, wie diese Messung und ihr Ergebnis aussehen werden. Bell selbst argumentierte, dass, selbst wenn deterministische Zufallszahlengeneratoren die Messungen auswählen, die Entscheidungen für das betreffende Objekt als tatsächlich frei angesehen werden können, da viele minimale Effekte die Entscheidungen der Maschine verändern. Es ist unwahrscheinlich, dass die verborgene Variable für dieselben kleinen Einflüsse empfindlich ist wie der Zufallszahlengenerator [71]. Auch die experimentellen Beweise widersprechen dem Superdeterminismus, denn bisher haben alle Bell-Tests ergeben, dass die Hypothese lokaler verborgener Variablen nicht mit dem Verhalten physikalischer Systeme vereinbar ist [72]. Und schließlich ist der Superdeterminismus aus rein logischer Sicht ein Zirkelschluss, da er im Kern davon ausgeht, dass das Universum deterministisch ist; folglich muss auch die Quantenphysik deterministisch sein.

Da es außerdem keine Möglichkeit gibt, die Teilchen des Computers von den übrigen Teilchen des Universums in der Simulation vollständig zu isolieren, werden die sich ändernden internen Zustände des Computers immer den Zustand des Universums beeinflussen, so dass eine exakte Simulation des Universums nicht möglich ist. Die dargelegten Argumente sind starke Indizien dafür, dass ein quantenphysikalisches Universum nicht-deterministisch und unvorhersehbar ist. Wir nennen dies im Folgenden die physikalische Vorhersagbarkeitsbeschränkung.

Die Argumente gegen die Berechenbarkeit und Vorhersagbarkeit zeigen deutlich, warum eine Simulation des Universums von innen heraus unmöglich ist und auch in ferner Zukunft nicht möglich sein wird, ganz gleich, wie leistungsfähig die Rechenanlagen werden. Für die Simulation eines Universums gelten andere Argumente.

B. Simulation eines Universums

In diesem Text bezieht sich die Simulation eines Universums auf die Simulation von Teilen des Universums oder eines Universums mit anderen physikalischen Gesetzen. Letzteres wäre keine Emulation, da das Ziel nicht darin besteht, das Verhalten des Universums zu imitieren. Die Simulation eines Universums umfasst sowohl die Simulation eines Universums von innen als auch die Simulation eines Universums von außen, wobei letztere auch die Simulation des Universums von außen einschließt, da für einen externen Programmierer das Universum ein Universum ist und ein externer Programmierer den gleichen, zuvor definierten rechnerischen Beschränkungen unterliegt, wenn er versucht, sein Universum zu simulieren. Dies gilt auch, wenn wir als externe Programmierer für intelligente (in Ermangelung eines besseren Wortes) Wesen in einem Universum erscheinen. Was die Berechenbarkeit betrifft, so ist die Simulation eines Universums durchaus möglich, und es gibt verschiedene Argumente, die die Hypothese stützen, dass wir selbst in einer Simulation eines Universums existieren. Wir unterscheiden zwischen der Simulation eines Universums von innen und von außen, wobei die Simulation von innen die exakte Simulation von Teilen des Universums durch einen internen Programmierer ist, z. B. dass wir eine Galaxie des Universums simulieren. Eine Simulation von außen ist ein externer Programmierer, der ein Universum von innen simuliert. Das Universum könnte z. B. eine solche Simulation sein. Der Computer kann in diesem Fall viel kleiner und weniger komplex sein, als er es sein müsste, wenn er das Universum simuliert, und die kleinsten logischen Informationseinheiten – z. B. Qubits – können aus mehreren physikalischen Teilchen oder Systemen zusammengesetzt sein.

• Die Simulation des Universums von innen durch einen internen Programmierer kann keine Simulation des Computers enthalten, der die Simulation ausführt, wenn tc<tn, wobei tn einen beliebigen Zeitschritt in der Simulation markiert, wegen des zuvor eingeführten Arguments der Unvorhersehbarkeit. Die Simulation eines Universums ohne den Computer, auf dem die Simulation abläuft, ist jedoch kein Widerspruch, abgesehen von anderen Einschränkungen. Ein von innen oder außen simuliertes Universum kann kleiner sein als das Universum des internen oder externen Programmierers. Die Simulation eines Universums von innen könnte zum Beispiel nur einige wenige Galaxienhaufen oder sogar nur eine Galaxie umfassen, in der eine intelligente Spezies lebt. Nach aktuellen Beobachtungen enthält das Universum schätzungsweise 1×1012-2×1012 Galaxien [73]. Wenn wir als interne Programmierer ein Universum simulieren müssten, weil die Berechnungsmöglichkeiten eingeschränkt sind, wäre es vernünftig, die Anzahl der astronomischen Objekte zu begrenzen. Auch wenn das Universum eines externen Programmierers unendlich ist, könnte eine Simulation eines Universums die Komplexität in Bezug auf die enthaltenen Objekte und die Größe begrenzen. Die vorherrschenden Theorien über die Entwicklung des Universums lassen den Schluss zu, dass seine Größe zunimmt und seine Expansionsrate sich beschleunigt, es aber dennoch endlich ist. Die Endlichkeit unterstützt das Argument, dass das Universum wirklich ein Universum ist, da die Simulation eines externen Programmierers durch die Rechenressourcen begrenzt ist. Außerdem würde das Rekursionsproblem zu einer geringeren Komplexität pro Simulation in der Hierarchie führen, da eine Simulation sxS={s1,…,sn} mit n→∞ durch die vom Computer in sx-1 auf der Hierarchieebene x-1 zur Verfügung gestellten Rechenressourcen begrenzt wäre (siehe Abb. 3). Das Argument ist eine Erweiterung der ersten Berechnbarkeitsbeschränkung, die bei der Simulation eines Universums Anwendung findet, in dem der Computer kleiner ist als das Universum und möglicherweise auch kleiner als das von ihm simulierte Universum.

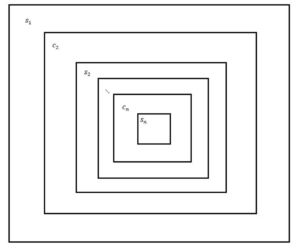
Abb. 3. Eine Simulationshierarchie, wobei s1 das Universum markiert, das eine Simulation sein kann (oder auch nicht). c2…n sind die Computer, auf denen die Simulationen s2…n laufen, von denen jeder kleiner ist als der Computer, auf dem er läuft.

• Die Simulation eines Universums von innen oder außen unterliegt denselben physikalischen Gesetzen wie eine Simulation des Universums. Wenn ein interner oder externer Programmierer beschließt, Teile seines Universums zu simulieren und damit ein Universum zu schaffen, verhindert die physikalische Vorhersagbarkeit, dass die Entwicklung der Simulation eines Universums mit Teilen des Universums identisch ist. Die durch die Quantenphysik bedingten Unsicherheiten in der Natur ermöglichen die Simulation eines Universums, das auf denselben physikalischen Gesetzen beruht wie das Universum. Die Entwicklung einer solchen Simulation könnte im Prinzip dem Universum ähnlich sein, muss aber nicht identisch sein. Zum Beispiel könnte die Mischung aus Materie, Antimaterie und dunkler Materie unterschiedlich sein, mit weniger oder mehr von jedem, oder ein Universum, in dem Antimaterie anstelle von Materie astronomische Objekte ausmacht. Wenn das Universum mehr als eines von beiden enthielte, wäre sein Schicksal in der fernen Zukunft oder sogar in der Vergangenheit ein anderes. Unter der Annahme, dass die Simulation eines Universums zu einer universellen Evolution führt, die unseren Beobachtungen ähnelt, ist es denkbar, dass sich in dieser Simulation eine intelligente Spezies entwickelt. Der zweite Hauptsatz der Thermodynamik besagt, dass die thermodynamische Entropie – der Zustand der Unordnung – in einem geschlossenen oder isolierten System (wie einem Universum) zunimmt, wenn sich dieses System entlang des Pfeils der Zeit fortbewegt. Im Gegensatz zu den ersten Annahmen bedeutet mehr thermodynamische Entropie mehr Rechenkomplexität und folglich auch mehr Rechenressourcen, die für die Simulation eines Universums benötigt werden. Eine Möglichkeit, sich die thermodynamische Entropie vorzustellen, ist die Anzahl der Konfigurationen, die ein Teilchen annehmen kann: Je mehr Möglichkeiten ein System hat, seine Teilchen anzuordnen, desto komplexer ist es. Je weiter sich ein Teilchen auf dem Pfeil der Zeit bewegt, desto mehr interagiert es mit anderen Teilchen und verschränkt sich mit anderen Teilchen, was zu einem komplexeren Universum führt. Nun gibt es einen Zwischenschritt, bei dem die Wechselwirkungen zwischen den Komponenten des Universums, z. B. auf atomarer oder molekularer Ebene, die thermodynamische Entropie lokal verringern und die Komplexität der Berechnungen weiter erhöhen. Das Leben ist ein gutes Beispiel: Jeder lebende Organismus benötigt Energie, um zu funktionieren, Zellen zu reproduzieren und seine Struktur zu erhalten. Eine Möglichkeit, wie sich thermodynamische Entropie auf lebende Organismen auswirkt, ist der Zellabbau oder der Zelltod. Der Stoffwechsel wirkt dem entgegen, indem er die Stoffe im Körper der Lebewesen chemisch umwandelt, z. B. indem er die Nahrung in Zwischen- und Endprodukte umwandelt. Diese biochemischen Prozesse bauen Körpersubstanzen auf, ab, ersetzen oder erhalten sie, erzeugen Energie für energieverbrauchende Tätigkeiten und erhalten so die Körperfunktionen und damit das Leben. Enzyme, die chemische Umwandlungen katalysieren, sind für den Stoffwechsel unerlässlich. Werden von außen aufgenommene Fremdstoffe umgewandelt, spricht man auch vom Fremdstoffwechsel. Die Umwandlung von organismusfremden Stoffen in organismuseigene Stoffe wird als Assimilation bezeichnet. Das Gegenteil ist die Dissimilation, der Abbau von organismuseigenen Stoffen. Zum Stoffwechsel gehört auch die Umwandlung von Schadstoffen in ausscheidbare Stoffe. Stoffwechselvorgänge können physikalisch als Tausch von freier Energie gegen Ordnung interpretiert werden: Lebende Organismen erhöhen ihre Ordnung und verbrauchen dabei Energie. Im Organismus nimmt die thermodynamische Entropie ab, während sie in der Umwelt zunimmt. Obwohl also die thermodynamische Entropie von a und des Universums im Laufe der Zeit global zunimmt, nimmt die Komplexität der Berechnungen aufgrund der zunehmenden Anzahl von Wechselwirkungen zwischen den Teilchen weiter zu, und zwar solange, wie komplexe Strukturen wie astronomische Objekte und/oder Leben entstehen und lokal erhalten werden. Geht man davon aus, dass eine intelligente Spezies in der Simulation irgendwann in der Lage ist, Galaxien und/oder größere Strukturen im Universum zu manipulieren, wird die Zunahme der Rechenkomplexität noch deutlicher ausfallen. Diesem Argument zufolge würde ein Computer, der zur Simulation eines Universums verwendet wird, einen Anstieg des Rechenaufwands verzeichnen, wenn sich die Simulation in der Zeit weiterentwickelt. Das Gleiche gilt für Simulationen in der Simulation, was auch durch die beiden in diesem Abschnitt vorgestellten Rekursionsargumente unterstützt wird. Ein paar Worte zum Zeitpfeil: Wir können drei Zeitpfeile [74] betrachten – den psychologischen Zeitpfeil, den thermodynamischen Zeitpfeil und den kosmologischen Zeitpfeil.
• Der psychologische Zeitpfeil bezieht sich auf unsere eigene Wahrnehmung, wie die Zeit im Universum und lokal voranschreitet, oder auf unsere Erinnerungen.
• Der thermodynamische Zeitpfeil bezieht sich auf die Zunahme der thermodynamischen Entropie im Universum. Auch wenn die thermodynamische Entropie lokal abnimmt, nimmt sie global gesehen immer zu. Egal, wie das Schicksal des Universums aussieht (siehe Kapitel V), die thermodynamische Entropie nimmt nicht ab. Wenn die Expansion ewig anhält, erwarten wir den Wärmetod des Universums oder das Big Chill [75]. Wenn das Universum erneut kollabiert, was als Big Crunch [76] bezeichnet wird, nimmt die thermodynamische Entropie ebenfalls nicht ab, sondern steigt weiter an, auch wenn die Raumzeit kollabiert.
• Der kosmologische Zeitpfeil bezieht sich auf die Richtung der Expansion des Universums. Er kann mit dem thermodynamischen Zeitpfeil verknüpft sein, wenn das Universum ewig weiter expandiert. Dieser Zeitpfeil würde sich umkehren, wenn das Schicksal des Universums der Big Crunch wäre.

Das vorgestellte Argument wird als dritte Rechenbarkeitsbeschränkung bezeichnet, da selbst bei der Simulation eines Universums ohne weitere Simulationen in der Hierarchie nach unten die Rechenkomplexität der Simulation aufgrund einer zunehmenden Anzahl von Teilchenwechselwirkungen entlang des Zeitpfeils und der energiebedingten Abnahme der lokalen Entropien zunehmen würde. Selbst wenn das Universum des externen Programmierers und der Computer, auf dem die Simulation abläuft, unterschiedlichen physikalischen Gesetzen unterliegen und die Simulation zu Beginn rechnerisch einfach ist, wird die rechnerische Komplexität zunehmen und, wenn genügend Zeit vergeht, die Rechenressourcen erschöpfen. Es sei gesagt, dass die äußere Zeit außerhalb der Simulation nicht mit der gleichen Geschwindigkeit ablaufen muss wie die innere Zeit innerhalb der Simulation: Selbst wenn die Simulation mit erhöhter Geschwindigkeit abläuft oder von einer äußeren Wahrnehmung auf die innere Zeitwahrnehmung beschleunigt wird, macht dies keinen Unterschied. Je nach dem Schicksal des Universums können wir unterschiedliche Entwicklungen der thermodynamischen Entropie beobachten. Wenn sich das Universum ewig weiter ausdehnt, wird die thermodynamische Entropie so weit fortschreiten, bis keine Teilchenwechselwirkungen mehr stattfinden können und somit den einzelnen Teilchen keine zusätzlichen Freiheitsgrade mehr hinzugefügt werden können. Ebenso wird die globale thermodynamische Entropie in einem Big-Crunch-Szenario weiter wachsen, aber die schrumpfende Oberfläche, die das Universum begrenzt, kann die Komplexität an der begrenzenden Oberfläche je nach ihrer Beschaffenheit reduzieren. Wenn der Computer, auf dem die Simulation abläuft, an dieselben physikalischen Gesetze gebunden ist wie die Simulation, kann die dritte Einschränkung der Berechenbarkeit aufgeschoben werden, wenn der Computer für die Simulation eines Universums größer ist als die Größe des Universums, was theoretisch möglich, aber aufgrund der Komplexität, die mit dem Bau eines solchen Systems verbunden ist, nicht sinnvoll ist.

• Eine weitere Einschränkung der physikalischen und rechnerischen Vorhersagbarkeit besteht darin, dass es unmöglich ist, den Computer, der ein Universum simuliert, von dem Universum zu trennen, selbst wenn der Computer nicht Teil der Simulation ist. Der Grund dafür sind Quantenvakuumfluktuationen, d. h. die Fähigkeit des Raums, Teilchen und ihre Antiteilchen scheinbar aus dem Nichts zu erzeugen. Die Grundlage für die quantenmechanische Möglichkeit der Teilchenerzeugung ist die Heisenbergsche Unschärferelation (Gl. 4), die in Bezug auf die Energie als Gl. 22 umformuliert werden kann und besagt, dass die Energie-Unschärfe multipliziert mit der Zeit-Unschärfe immer kleiner sein muss als eine Naturkonstante in einem kleinen Raumvolumen – die Plancksche Konstante.

 

tE≥2 (22)

 

ΔA〈A〉∂tE≥2 (23)

 

In Gl. 23 kann ∆t als die Zeit interpretiert werden, in der sich ein Quantenvakuumzustand in Bezug auf eine Beobachtungsgröße A signifikant ändert. Diese Unschärferelation ist eine direkte Folge des Welle-Teilchen-Dualismus und gilt grundsätzlich für alle Elementarteilchen. Quantenfluktuationen treten auf, wenn sich ein Teilchen-Antiteilchen-Paar kurzzeitig bildet, ohne diese Unschärferelation zu verletzen. Eine Folge der Quantenfluktuation ist zum Beispiel, dass es kein absolutes Vakuum geben kann. Auch werden ständig Teilchen-Antiteilchen-Paare im “leeren Raum” erzeugt und verschwinden wieder. Experimentelle Belege für diese Situation liefert beispielsweise der Casimir-Effekt, bei dem nahe beieinander liegende Metallplatten im Vakuum Kräfte aufeinander ausüben. Mit Hilfe von Quantenfluktuationen lässt sich auch die Entstehung von Teilchen in der Nähe von Schwarzen Löchern, genauer gesagt an deren Schwarzschild-Radius, erklären. Auf diese Weise kann eines der beiden Teilchen aus dem Schwarzen Loch entkommen, wenn die Teilchenbildung in einem Bereich um diesen Radius stattfindet. Im Allgemeinen ist die innere Komplexität von Schwarzen Löchern noch nicht geklärt. Nach unserem derzeitigen Kenntnisstand kann Quanteninformation nicht zerstört werden, so dass Schwarze Löcher in ihrem Inneren ungeheuer komplex sein müssten. In bestimmten kosmologischen Modellen wird auch die Entstehung des Universums im Urknall als Quantenfluktuation betrachtet. Wenn man nun einen Computer verwendet, um ein Universum von innen heraus als Teil des Universums genau zu simulieren, würde man auf eine Mischung aus physikalischen und rechnerischen Vorhersagebeschränkungen stoßen: Der interne Zustand des Computers würde durch das zufällige Auftauchen von Teilchen beeinflusst, die durch Quantenfluktuationen im Universum verursacht werden, was ihn daran hindert, den zukünftigen Zustand von Teilen des Universums genau vorherzusagen. Von nun an wird diese Einschränkung als kombinierte Vorhersagebeschränkung bezeichnet.

• Eine genaue Simulation eines Universums sowohl von innen als auch von außen kann auch zu dem Rekursionsproblem führen, das in der ersten Einschränkung der Berechenbarkeit beschrieben wird. Wenn wir als externe Programmierer Teile des Universums, z. B. eine Reihe von Galaxien oder Galaxienhaufen, genau simulieren, dann ist die Frage, ob wir beabsichtigen, Leben zu simulieren, eine wichtige Frage. Wenn das Leben Teil der Simulation ist – eine Annahme, die vernünftig erscheint, wenn die Simulation genau ist -, dann ist das Entstehen einer intelligenten Spezies wahrscheinlich. Falls dies geschieht und die Simulation genau ist, liegt es nahe, dass die intelligente Spezies in dem Teiluniversum auch die Absicht hat, das Universum zu simulieren. Bei der Simulation eines Universums ist die Simulation des Computers, der die Simulation ausführt, nicht erforderlich, und daher verursacht der für die Simulation verwendete Computer keine Rekursivität, wie sie in der ersten Berechnbarkeitsbeschränkung beschrieben wird; eine Spezies in der Simulation, die beabsichtigt, ein Universum zu simulieren, wird jedoch einen Computer für die Ausführung der Aufgabe verwenden, was wiederum zu einer hierarchischen Reihe von Simulationen führt. Der Computer auf der obersten Ebene müsste die Rechenressourcen für die Berechnung einer Reihe von Simulationen S ={s1,…,sn} mit n→∞ bereitstellen, woraus sich die erste Berechnbarkeitsbeschränkung ergibt, sobald eine Simulation auf einer bestimmten Ebene n ausgeführt wird. Lässt man alle anderen Einschränkungen außer Acht, kann man argumentieren, dass das Leben im Universum möglicherweise von einem externen Programmierer eingeführt wurde, anstatt von selbst zu entstehen, und dass dies eine Rekursion verhindern würde. Es liegt jedoch auf der Hand, dass eine künstlich eingeführte intelligente Spezies auch in Erwägung ziehen würde, ein Universum zu simulieren und eine intelligente Spezies in eine solche Simulation einzuführen, vorausgesetzt, dass eine solche Spezies nicht auftaucht. Auch in diesem Fall würde die erste Einschränkung der Berechenbarkeit eintreten. Die vorgestellte Argumentation erstreckt sich auf die erste Einschränkung der Berechenbarkeit, die sich auf die Simulation von komplexem Leben beschränkt.

Die in diesem Kapitel dargelegten Argumente zeigen, dass selbst wenn die Absicht besteht, nur Teile des Universums exakt zu simulieren, mehrere Einschränkungen uns daran hindern, dies zu tun. Die Argumente zeigen deutlich, dass eine Simulation eines Universums von innen heraus nicht möglich ist, ganz gleich, wie leistungsfähig die Computer werden und ob die für die Simulation verwendeten Computer Quantencomputer sind. Es gibt jedoch keine Beschränkungen, die die Simulation eines Universums von außen verhindern, also eines Universums, das sich physikalisch wie das Universum verhält, aber nicht mit ihm identisch ist. Wenn man all dies zusammennimmt, können Experimente entwickelt werden, um zu überprüfen, ob wir in einer Simulation leben und ob ein externer Programmierer existiert oder nicht.

VII. DIE SCHÖPFER-EXPERIMENTE

Wenn es einen externen Programmierer gibt und dieser das Universum erschaffen hat, kann der externe Programmierer

als Schöpfer betrachtet werden, der in den verschiedenen Religionen unterschiedliche Formen annimmt. Auf die Religion soll in diesem Zusammenhang nicht weiter eingegangen werden, da es uns um die Verifizierung oder Widerlegung der Simulationshypothese geht. Das primäre Ziel des skizzierten Experiments ist es, Hinweise darauf zu finden, ob das Universum und alles darin, einschließlich der Menschen und möglicherweise anderer intelligenter Wesen, von einem externen Programmierer geschaffen wurden und Teil einer Simulation sind. Die Hypothese für die folgenden Experimente ist klar und einfach: “Wir leben nicht in einem simulierten Universum und sind keine simulierten Wesen”. Bevor wir die Experimente skizzieren, sollen einige Annahmen, die zu Beginn von Kapitel VI gemacht wurden, noch einmal hervorgehoben werden.

1. Wir haben ein vollständiges Verständnis der physikalischen Gesetze, die die Entwicklung des Universums und seine Zusammensetzung bis hin zur physikalischen Ebene X bestimmen.
2. Die Gesetze der Quantenphysik sind die grundlegendsten physikalischen Gesetze. Diese Annahme steht auf soliden experimentellen Füßen, und wir sind ziemlich sicher, dass dies zumindest für die starke und schwache Wechselwirkung und den Elektromagnetismus zutrifft. Anders verhält es sich mit der Verbindung von allgemeiner Relativitätstheorie und Quantenphysik – zum Zeitpunkt der Veröffentlichung dieses Artikels wurde noch keine Theorie der Quantengravitation vorgeschlagen, die experimentell überprüft werden kann.
3. Es spielt keine Rolle, ob ein externer Programmierer beschließt, ein Universum zu simulieren, in dem dieselben physikalischen Gesetze gelten wie in seinem Universum oder eine andere Reihe physikalischer Gesetze. Sobald wir als externe Programmierer agieren und unsere Simulation auf die in unserem Universum vorherrschenden physikalischen Gesetze stützen, sind die Handlungen nachfolgender Programmierer in einer potenziell entstehenden Simulationskette mögliche Beobachtungen, nach denen wir im Universum Ausschau halten müssen.

In Kapitel VI haben wir mehrere Einschränkungen für die Erstellung einer Simulation des Universums und/oder eines Universums skizziert, die wir im Folgenden kurz zusammenfassen:

• Einschränkung der Vorhersagbarkeit des Computers: Wenn der Computer den Zustand des Universums zum Zeitpunkt t1 in tc vorhersagt, sagt er auch seinen eigenen internen Zustand zum Zeitpunkt tr voraus. Wenn der Computer zum Zeitpunkt tc aufgefordert wird, den Zustand des Universums zum Zeitpunkt t2 vorherzusagen, wird er seine Vorhersagen auf den Zustand des Universums, einschließlich seiner eigenen internen Konfiguration zum Zeitpunkt t1, stützen. Da jedoch tc<t1 ist, würde der Computer beginnen, seine interne Konfiguration zu ändern, um den Zustand des Universums bei t2 vorherzusagen, bevor t1 erreicht ist, und seine ursprünglichen Vorhersagen über seinen internen Zustand bei t1 sind nicht korrekt, wenn t1 erreicht ist.
• Beschränkung der physikalischen Vorhersagbarkeit: Es ist unmöglich, das Universum vollständig zu simulieren, da die Quantenphysik der Vorhersagbarkeit physikalischer Systeme mehrere Beschränkungen auferlegt. Selbst wenn der Computer, der die Simulation durchführt, in seinem internen Zustand ein Teilchen eines bestimmten Typs verwenden würde, um ein anderes Teilchen desselben Typs zu simulieren, verhindern die Unschärferelation und die Wellennatur der Teilchen, dass der Computer exakte Vorhersagen machen kann. Da es außerdem keine Möglichkeit gibt, die Teilchen des Computers vollständig von den übrigen Teilchen des Universums in der Simulation zu trennen, wird der sich ändernde interne Zustand des Computers immer den Zustand des Universums beeinflussen, wodurch eine Simulation des Universums unberechenbar wird.
• Erste Einschränkung der Berechenbarkeit: Jeder simulierte Computer müsste auch das Universum simulieren, einschließlich sich selbst, was eine Rekursion darstellt. Die Rekursion ist nicht nur rechenaufwendig, sondern führt auch zur generellen Unberechenbarkeit der Simulation, da die verfügbaren Rechenressourcen zur Berechnung einer Reihe von Simulationen S=s1,…,sn mit n→∞ verwendet werden müssen. Entweder würden dem Computer in s1 irgendwann die Ressourcen ausgehen, oder die Rechenressourcen in sn würden nicht ausreichen, um eine weitere Simulation sn + 1 durchzuführen. Eine Erweiterung dieser Einschränkung wurde eingeführt, wenn es darum geht, ein Universum und astronomische Objekte und/oder Leben zu simulieren: Wenn intelligente Spezies dazu neigen, ein Universum und alles Leben darin zu simulieren, kann man davon ausgehen, dass jede simulierte Spezies dieser Tendenz folgen wird. Auch hier würde die auftretende Rekursion zu einer geringeren Komplexität pro Simulation in der Hierarchie führen, da eine Simulation sxS=s1,…,sn mit n→∞ durch die vom Computer in sx-1 auf der Hierarchieebene x-1 zur Verfügung gestellten Rechenressourcen begrenzt wäre.
• Zweite Einschränkung der Berechenbarkeit: Ein Computer, der eine Simulation des Universums von innen heraus durchführt, müsste alle Teilchen des Universums, von denen wir derzeit annehmen, dass es 1078-1082 sind, in seinem internen Zustand darstellen. Der Bau eines solchen Computers würde mindestens 1078-1082 Teilchen erfordern; daher ist eine solche Simulation unmöglich.
• Dritte Einschränkung der Berechenbarkeit: Selbst bei der Simulation eines Universums ohne weitere Simulationen in der Hierarchie nach unten würde die Rechenkomplexität der Simulation aufgrund der zunehmenden Anzahl von Teilcheninteraktionen entlang des Zeitpfeils und der energiebedingten Verringerung der lokalen Entropien zunehmen, selbst wenn die globale thermodynamische Entropie weiter zunimmt. Da intelligente Spezies in einer Simulation dazu neigen würden, Simulationen mit komplexen astronomischen Objekten und Leben zu erstellen, würde sich die kumulative Komplexität der Simulationen in der unteren Simulationshierarchie summieren und alle primären Rechenressourcen aufbrauchen, die der Simulation auf der obersten Ebene zur Verfügung stehen.
• Kombinierte Vorhersagbarkeitsbeschränkung: Aufgrund von Quantenvakuumfluktuationen würde der interne Zustand des Simulationscomputers durch das zufällige Auftauchen von Teilchen beeinflusst, das durch Quantenfluktuationen im Universum (von dem der Computer ein Teil ist) verursacht wird, was ihn daran hindert, den zukünftigen Zustand von Teilen des Universums genau vorherzusagen.

Ein Experiment, das bestätigen oder widerlegen soll, dass das Universum und alles darin keine Simulation ist, erfordert, dass wir ein Universum simulieren, das sich physikalisch wie das Universum verhält. Aufgrund der rechnerischen, physikalischen und kombinierten Einschränkungen der Vorhersagbarkeit sowie der ersten und zweiten Einschränkung der Berechenbarkeit kann die Simulation nicht einmal Teile des Universums nachahmen, sondern nur die physikalischen Gesetze, von denen wir in unserer ersten und zweiten Annahme behaupten, sie vollständig und bis ins kleinste Detail verstanden zu haben. Jede exakte Simulation eines Universums darf nicht mit einem beliebigen Zustand zu einem beliebigen Zeitpunkt beginnen, sondern mit dem Beginn der Raumzeit – dem Urknall, wie wir ihn heute verstehen. Ein wichtiger Aspekt einer solchen Simulation ist, dass wir sie beschleunigen können, indem wir feststellen, welche auftretenden Phänomene statistisch relevant und keine zufälligen Erscheinungen sind. Die folgenden Beobachtungen können in einer solchen Simulation gemacht werden:

• In der Simulation taucht intelligentes Leben auf: Wenn in der Simulation intelligentes Leben entsteht, und zwar mit statistischer Relevanz über viele Simulationsdurchläufe hinweg, können wir daraus schließen, dass das Leben im Universum kein Zufall ist. Das Auftauchen von Leben allein ist jedoch kein Beweis dafür, dass das Universum und alles darin eine Simulation ist. Wenn das intelligente Leben in der Simulation nicht die Absicht hat, ein Universum zu simulieren, können wir dies als Argument dafür verwenden, dass wir nicht in einer Simulation leben. Wenn jedoch das intelligente Leben in der Simulation sein Universum simuliert, ist dies ein Hinweis darauf, dass das Universum und alles darin eine Simulation ist, da das Verhalten in jeder Simulation in der Simulationshierarchie sxS=s1,…,sn mit n→∞ nachgeahmt wird.
• Intelligentes Leben kommt in der Simulation nicht vor: Wenn in der Simulation kein intelligentes Leben entsteht, und zwar nicht mit statistischer Relevanz über viele Simulationsläufe hinweg, können wir entweder schlussfolgern, dass das Entstehen von Leben im Universum ein Zufall war oder dass Leben von einem externen Programmierer künstlich eingeführt wurde. Wenn kein Leben entsteht und wir als der externe Programmierer auftreten und intelligentes Leben in die Simulation einführen, können wir feststellen, dass das künstlich eingeführte Leben beabsichtigt, sein Universum zu simulieren. Wenn sie das tun, ist es wahrscheinlich, dass auch in ihrer Simulation kein intelligentes Leben auftaucht und sie es künstlich einführen.

Beide Situationen sind nicht schlüssig, ob wir in einer Simulation leben, aber wir können die Beobachtungen nutzen, um das Experiment weiter zu entwickeln. Wenn eine intelligente Spezies in einer Simulation, unabhängig davon, ob sie entstanden ist oder künstlich in die Simulation eingeführt wurde, eine Simulation ihres Universums erstellt, die intelligentes Leben enthält, deutet dies stark darauf hin, dass wir uns bereits in einer Kette von Simulationen befinden. Nun zieht jede weitere Simulation Rechenressourcen von der darüber liegenden Ebene ab, und unter der vereinfachenden Annahme, dass jede Simulation die ihr maximal zur Verfügung stehende Rechenleistung nutzt, muss jede Simulation weiter unten in der Simulationshierarchie den ersten und dritten Rechenbarkeitsbeschränkungen folgen und eine geringere Komplexität und/oder einen geringeren Inhalt aufweisen. Aufgrund der immer stärker werdenden Teilcheninteraktionen entlang des Zeitpfeils und der lokalen Abnahme der Entropien in jeder Simulation ist jede Simulation zudem mit einem immer höheren Bedarf an Rechenressourcen verbunden. Die Rechenressourcen auf jeder Ebene, selbst auf der obersten Ebene, müssen begrenzt werden, entweder durch Bedingungen oder durch Ressourcen, es sei denn, die Größe des Computers ist größer als die Größe des Universums, das er simuliert. Auch wenn jede Simulation auf der unteren Ebene der Simulationshierarchie weniger komplex ist als die vorherige, nimmt die Komplexität jeder Simulation sxS=s1,…,sn auf der unteren Ebene der Simulationshierarchie mit der Zeit zu, da ihre globale thermodynamische Entropie zunimmt und die lokale Entropie abnimmt, unabhängig vom Schicksal des jeweiligen simulierten Universums. Wenn wir an einer Kette von Simulationen teilnehmen, wird die sehr ferne Zukunft in unserer simulierten Zeit (die nicht mit der gleichen Geschwindigkeit ablaufen muss wie die Zeit des externen Programmierers) die Erschöpfung der Rechenressourcen auf jeder Ebene und damit die Zunahme der thermodynamischen Entropie auf jeder Ebene aufhalten. Wenn die thermodynamische Entropie (und damit die Zeit) auf einer beliebigen Ebene angehalten wird, kommen auch alle Entropien in Simulationen weiter unten in der Hierarchie sofort zum Stillstand. Gemäß der zweiten und dritten Einschränkung der Berechenbarkeit wird die Komplexität im/a-Universum zunehmen, unabhängig vom Schicksal des/a-Universums, und die Erschöpfung der Rechenressourcen ist unvermeidlich, wenn der Computer kleiner ist als das von ihm simulierte Universum, es sei denn, die globale thermodynamische Entropie wird umgekehrt. Nach unserem derzeitigen Kenntnisstand ist es nicht möglich, die thermodynamische Entropie im Universum global umzukehren, aber wenn es sich um eine Simulation handeln würde, hätte ein externer Programmierer sicherlich die Möglichkeit, dies zu tun, und wir hätten die Möglichkeit, dies zu tun, wenn wir die Simulation eines Universums in unserem Universum ausführen würden. Es gibt vielleicht noch andere Möglichkeiten, die Komplexität zu reduzieren, z. B. durch eine drastische Verringerung der Anzahl der Objekte in der Simulation, wenn die globale thermodynamische Entropie zunimmt. Bleiben wir bei dem Beispiel der thermodynamischen Entropiereduzierung durch einen externen Programmierer: Wenn wir ein Universum s1 simulieren und in dieser Simulation intelligentes Leben entsteht, das ein Universum s2 simuliert, werden dieselben Rechenbeschränkungen, die in s1 auftreten, auch in s2 auftreten. In diesem Experiment wirken wir als externe Programmierer der Erschöpfung der Rechenressourcen in s2 – dem von uns simulierten Universum – entgegen, indem wir die globale thermodynamische Entropie des von uns simulierten Universums umkehren, was zu einer geringeren Komplexität, einer steigenden Temperatur, weniger komplexen Molekülen und mehr führt. Eine Umkehrung der globalen thermodynamischen Entropie erfordert keine Umkehrung der lokalen Entropien. Mit anderen Worten: Eine abnehmende globale thermodynamische Entropie erfordert keine zunehmende lokale thermodynamische Entropie. Wenn wir nun beobachten, dass dies auch in s2 für s3 geschieht, wobei s3 die Simulation eines Universums ist, das in s2 läuft, und weiter unten in der hierarchischen Simulationskette, können wir schlussfolgern, dass die Umkehrung der thermodynamischen Entropie in einer Simulationskette, um eine Erschöpfung der Rechenressourcen zu verhindern und sie am Leben zu erhalten, ein erwartetes Verhalten ist. Da der thermodynamische Pfeil der Zeit uns daran hindert, die globale thermodynamische Entropie im Universum zu verringern, haben wir keine akzeptierten Theorien über das Schicksal des Universums in einem solchen Szenario. Sollten wir jedoch eine Abnahme der globalen thermodynamischen Entropie beobachten, die durch physikalische Gesetze nicht erklärbar ist, würde dies den Schluss zulassen, dass wir in einer Simulation leben, die von einem externen Programmierer gesteuert wird.

Die Verringerung der thermodynamischen Entropie zur Verringerung der Rechenkomplexität ist nur ein denkbares Beispiel für Maßnahmen eines externen Programmierers, die zu beobachtbaren Folgen in einer Simulation führen können. Es ist denkbar, dass ein externer Programmierer noch gravierendere Veränderungen grundlegender physikalischer Gesetze vornimmt, wie z. B. die Verdichtung räumlicher oder zeitlicher Dimensionen. In der Physik ist die Suche nach einer Theorie von allem, die alle physikalischen Phänomene von der subatomaren bis zur kosmologischen Skala erklärt, eines der schwierigsten Probleme. Ein Kandidat für eine Theorie von allem ist die M-Theorie [77-79], in der die Stringtheorien zusammengefasst sind [80]. Genauer gesagt ist die M-Theorie ein Versuch, die Stringtheorie zu erweitern und zu verallgemeinern und ist die elfdimensionale vereinheitlichte Theorie der fünf Stringtheorien und der Supergravitation. Es wurde gezeigt, dass die fünf Stringtheorien nur spezielle Grenzfälle der M-Theorie sind [81]. Selbst heute, da die M-Theorie Gegenstand aktiver Forschung ist und nicht mathematisch beschrieben werden kann, offenbart sie bereits bemerkenswerte Eigenschaften der Strings, der Raumzeit und des Universums. Sie vereinigt nicht nur die vier Grundkräfte, sondern bringt auch die Quantenphysik mit der allgemeinen Relativitätstheorie in Einklang. Eine der weitreichendsten Konsequenzen, die sich daraus ergeben, ist die Erkenntnis, dass die fundamentalen Bausteine des Universums nicht ausschließlich eindimensionale Strings sind, sondern mehrdimensionale Objekte, sogenannte Branes. Unsere Wahrnehmung und aktuelle Experimente führen dazu, dass wir das makroskopische Universum mit einer vierdimensionalen Raumzeit beschreiben, und hier sehen wir eine Diskrepanz zur M-Theorie, die zehn Raumdimensionen und eine Zeitdimension aufweist. Man nimmt an, dass die sieben unbeobachteten Raumdimensionen auf der Planck-Skala angesiedelt sind, zu der die heutigen Teilchenbeschleuniger keinen Zugang haben. Heutige Teilchenbeschleuniger erzeugen Energien um 1013 eV, die Planck-Energie beträgt jedoch 1,2 × 1019 GeV. Es wurde gezeigt, dass die Supergravitation nicht nur bis zu elf Dimensionen zulässt, sondern in dieser maximalen Anzahl von Dimensionen auch am elegantesten ist, wodurch die Erweiterung der gemeinsamen 10-dimensionalen Raumzeit der Stringtheorien zur 11-dimensionalen Raumzeit der M-Theorie zustande kam. Unter der Annahme, dass das Universum zum Zeitpunkt des Urknalls 11 makroskopische Raumzeitdimensionen aufwies, könnte ein externer Programmierer die Verdichtung (Abb. 4) nutzen, um die Rechenkomplexität mit zunehmender thermodynamischer Entropie entlang des Zeitpfeils zu verringern.

Abb. 4. Verdichtung des Raums M×C über dem kompakten C

Es wird angenommen, dass einige der zusätzlichen Dimensionen Kreise bilden oder sich in sich selbst schließen, was theoretisch unendliche oder sehr große Dimensionen auf Dimensionen endlicher Länge reduzieren würde. Eine gängige Annahme darüber, warum einige Raum-Zeit-Dimensionen verdichtet sein könnten, ist, dass die kosmische Inflation nur einige der Dimensionen vergrößert und andere aus unbekannten Gründen auf der Planck-Skala zu Kreisen zusammengerollt hat. Wenn dies zutrifft, sind die vier Kräfte, die wir in unserer vierdimensionalen Raumzeit wahrnehmen, lediglich Manifestationen der gleichen vereinheitlichten Kraft einer höherdimensionalen Raumzeit. Da physikalische Systeme zur Einfachheit neigen, wäre eine einzige vereinheitlichte Kraft natürlich “vernünftiger” als vier verschiedene Kräfte. Dennoch kann man davon ausgehen, dass ein externer Programmierer in der Lage wäre, die Dimensionen der Raumzeit zu verdichten oder sogar zu eliminieren, wobei die vollständige Eliminierung der Dimensionen vermutlich katastrophaler wäre. Darüber hinaus kann die Verdichtung auf eine vierdimensionale Raumzeit lokal sein, unabhängig davon, ob sie ein inhärentes Merkmal des Universums ist oder von einem externen Programmierer verursacht wurde. Andere Raum-Zeit-Blasen können sehr wohl höher- oder niederdimensional sein. Sollte der Mensch jemals höherdimensionale Raumzeitregionen entdecken, und sollten sich diese vor allem in Gebieten befinden, die nicht von komplexen astronomischen Objekten bevölkert sind, könnte dies darauf hindeuten, dass die Raumzeit in anderen Regionen künstlich verdichtet wurde und wir an einer Simulationskette teilnehmen.

Eine andere Form der Dimensionalitätsreduktion zur Aufschiebung der zweiten Berechnbarkeitsbeschränkung ist das holographische Universum [58, 59]. Dabei handelt es sich um die Hypothese, dass es für jede Beschreibung der Dynamik eines Raum-Zeit-Bereichs eine äquivalente Beschreibung gibt, die nur am Rand dieses Bereichs lokalisiert ist. Infolgedessen hängt die maximal mögliche Entropie einer Raumregion nicht von ihrem Volumen, sondern nur von ihrer Oberfläche ab, wie im Fall der Bekenstein-Hawking-Entropie von Schwarzen Löchern [54, 57]. Das holographische Prinzip lieferte eine Interpretation der Entropie Schwarzer Löcher und wurde sogar durch sie motiviert. Unter Berücksichtigung der Gravitation kann der Informationsgehalt – die Anzahl der möglichen Anordnungen von Teilchen und Feldern – keine rein lokale Größe sein, da er proportional zum Volumen wäre. Die Fläche des Ereignishorizonts eines Schwarzen Lochs – die durch den Schwarzschild-Radius gebildete Grenzfläche des Schwarzen Lochs – ist ein direktes Maß für die Entropie bzw. den Informationsgehalt des eingeschlossenen Raumvolumens und damit für die darin enthaltenen Massen. Ein Schwarzes Loch stellt immer die maximal mögliche Konzentration von Materie in einer Raumregion und damit die Obergrenze der möglichen Entropie oder Information in dem von ihm eingenommenen Raumvolumen dar. Das holografische Prinzip besagt, dass jede Information, die über die Oberfläche des Ereignishorizonts eines Schwarzen Lochs hinausgeht, vollständig auf der vom Schwarzschild-Radius aufgespannten Grenzfläche kodiert wird, ähnlich wie ein zweidimensionales Hologramm, das dreidimensionale Bildinformationen enthält. Da der Schwarzschildradius eines Schwarzen Lochs direkt proportional zu seiner Masse ist, wächst das kodierbare Volumen schneller als die Oberfläche. Um das vierfache Volumen zu kodieren, steht nur die doppelte Fläche zur Verfügung. Das bedeutet, dass die Informationsdichte eines Raumgebiets mit zunehmendem Volumen abnimmt, so wie die durchschnittliche Massendichte eines Schwarzen Lochs analog mit der Größe abnimmt, oder kurz gesagt, dass Information gleich Fläche ist. Das wiederum lässt den Schluss zu, dass zum Beispiel unsere 4-dimensionale Raumzeit einschließlich ihrer physikalischen Gesetze an ihrer 3-dimensionalen Grenze kodiert sein könnte. Es wurde gezeigt, dass ein theoretisches Universum, das durch die Superstringtheorie in einer Anti-de-Sitter-Raumzeit [82] beschrieben wird, einer Quantenfeldtheorie entspricht, die an ihrem Rand operiert [83]. Dies wurde zunächst für die 5-dimensionale Anti-De-Sitter-Raumzeit [84] bestätigt und zeigt, dass es für Wesen in einem Universum unmöglich ist, festzustellen, ob sie in einem 4-dimensionalen Universum mit einer Quantenfeldtheorie oder in einem 5-dimensionalen Universum mit einer Stringtheorie existieren. Ein externer Programmierer könnte sich diese Tatsache zunutze machen und ein komplexeres, höherdimensionales Universum als physikalische Theorien kodieren, die auf seiner niederdimensionalen Grenzfläche funktionieren, oder umgekehrt (was kein Hologramm ist). Der letztere Fall könnte besonders interessant sein, um die Rechenkomplexität zu verringern, da nur die physikalischen Gesetze in einer höherdimensionalen Raumzeit kodiert werden könnten. Das Universum und seine Entwicklung könnten sich auf seiner niederdimensionalen Grenzfläche abspielen. Ein externer Programmierer könnte die physikalischen Gesetze definieren, und die Regeln für die Evolution könnten in der höherdimensionalen Raumzeit definiert und auf die Grenzfläche projiziert werden, wo sie die Evolution eines niederdimensionalen Universums steuern. Wenn Experimente [85] zeigen, dass das holographische Universum wahr ist, kann dies als Hinweis darauf interpretiert werden, dass wir an einer Simulationskette teilnehmen.

Sicherlich gibt es noch viele weitere drastische Möglichkeiten, die sich ein externer Programmierer ausdenken kann, um die Rechenkomplexität des Universums zu reduzieren, und nicht alle von ihnen sind möglicherweise nachweisbar. Zusammenfassend können wir bei der Durchführung von Simulationen eines Universums folgende Szenarien beobachten (die alle viele Male ausgeführt werden, um die statistische Signifikanz der Ergebnisse zu gewährleisten):

• Intelligentes Leben taucht in unserer Simulation eines Universums und weiter unten in der Simulationshierarchie auf: Wenn dies der Fall ist, können wir davon ausgehen, dass wir in einer Kette von Simulationen leben, da die Simulation eines Universums mit intelligenten Spezies, die die Absicht haben, ein Universum zu simulieren, ein normales Verhalten darstellt. In diesem Szenario können weitere Beobachtungen gemacht werden:
  • Die Beobachtung grundlegender und schwerwiegender physikalischer Eingriffe durch externe Programmierer in eine Kette von Simulationen, wie z. B. eine Umkehrung der globalen thermodynamischen Entropien, eine Verdichtung der Dimensionen, die Umsetzung des holografischen Prinzips in verschiedenen Formen, ein absichtlich herbeigeführter Big Crunch oder Ähnliches. Die Beobachtung solch dramatischer Eingriffe lässt den Schluss zu, dass wir an einer Simulationskette teilnehmen.
  • Die Beobachtung einer Umkehrung der thermodynamischen Entropien oder einer Verdichtung der Dimensionen, der Umsetzung des holographischen Prinzips in verschiedenen Formen, eines absichtlich herbeigeführten Big Crunch oder Ähnlichem in einer Kette von Simulationen, die viele Male ausgeführt werden, ist statistisch nicht relevant: Wir sind einzigartig in der Umsetzung solch drastischer physikalischer Eingriffe in unserer Simulation s1, was den Schluss zulässt, dass wir nicht an einer Simulationskette teilnehmen oder dass wir die ersten in einer Simulation sind, die sich um die Erschöpfung der Rechenressourcen von Simulationen in der unteren Simulationshierarchie kümmern. Wenn sich alles intelligente Leben in der Simulationshierarchie anders verhält als wir im Sinne einer thermodynamischen Entropieumkehr (oder ähnlichem), können wir daraus schließen, dass wir die ersten externen Programmierer sind und nicht selbst in einer Simulation leben.
• Es entsteht keine weitere Simulationshierarchie, obwohl in unserer Simulation eines Universums intelligente Spezies auftauchen: Aus diesem Szenario können wir schließen, dass wir die ersten externen Programmierer sind und selbst nicht in einer Simulation leben.
• In unserer Simulation eines Universums entsteht kein intelligentes Leben, obwohl alle anderen physikalischen Verhaltensweisen in der Simulation mit denen des Universums identisch sind: Aus diesem Szenario können wir entweder folgern, dass wir die ersten sind, die eine Simulation durchführen, und dass die Entstehung von Leben, wie wir es kennen, ein Zufall war, oder dass ein externer Programmierer Leben in das Universum eingeführt hat und wir in einer Simulation leben. Wenn wir nun selbst eine Simulation eines Universums durchführen und das Entstehen einer Simulationshierarchie beobachten, nachdem wir künstlich intelligentes Leben eingeführt haben, und keiner der Programmierer in der Hierarchie es einführen muss, weil es von selbst entsteht, könnten wir zu dem Schluss kommen, dass wir nicht in einer Simulation leben und die ersten sind, die ein Universum simulieren. Wenn eine Simulationshierarchie entsteht, bei der simuliertes intelligentes Leben in jeder neuen Simulation selbst künstlich intelligentes Leben einführt, könnten wir zu dem Schluss kommen, dass wir uns in einer Kette von Simulationen befinden.

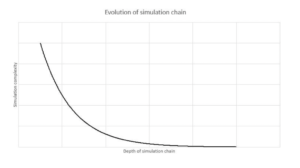
Abb. 5. Weiter unten in der Simulationskette ist die Komplexität jeder neuen Simulation geringer als die der vorhergehenden, da die Simulation sx-1 nicht nur sich selbst ausführt, sondern auch den für die Ausführung von sx verwendeten Computer enthält.

Wenn wir ein Szenario beobachten, in dem intelligente Spezies und eine Simulationshierarchie entstehen (mit oder ohne unser Zutun), wissen wir aufgrund der ersten und dritten Berechnbarkeitsbeschränkung, dass die Komplexität jeder Simulation in der Hierarchie mit der Zeit zunehmen wird. Wir wissen auch, dass jede Simulation in der Hierarchie weniger komplex sein wird als die vorherige – sx+1 ist weniger komplex als sx, da ein Computer, der sx+1 mit gleicher Komplexität wie sx simuliert, aus mindestens so vielen Teilchen bestehen müsste wie sx selbst (Abb. 5). Irgendwann in der Hierarchie wird die letzte Simulation sn auftauchen, da die Komplexität, die mit der Erstellung weiterer Simulationen verbunden ist, aufgrund der unzureichenden Komplexität von sn nicht erreicht werden kann. Wir können auch mit einer einfachen Simulation beginnen und die Komplexität erhöhen. Auf diese Weise können wir feststellen, welche die erste Simulation mit ausreichender Komplexität ist, damit intelligentes Leben, das ein Universum simuliert, entstehen kann. Durch den Vergleich der beiden Simulationen, der vorletzten in der Simulationskette – sn-1, in der eine intelligente Spezies noch ein Universum sn simuliert -, und der ersten, die eine ausreichende Komplexität aufweist, um eine intelligente Spezies zu beherbergen, die ein Universum smin simuliert, können wir Folgendes beobachten und feststellen:

• Die beiden Universen haben viele Gemeinsamkeiten in ihrer Entwicklung, ihrer Struktur und ihrem Inhalt: Wir stellen fest, dass es keine Rolle spielt, ob wir die Simulationskette bis zur geringsten Komplexität entwickeln lassen oder ob wir eine Simulation mit der geringsten Komplexität beginnen, die für die Entstehung von intelligentem Leben erforderlich ist, indem wir ein Universum direkt simulieren – die Universen mit der geringsten Komplexität sind identisch. Unter der Annahme, dass smin dem Universum ähnlich ist, und beide einander ähnlich sind, ist sn-1 auch dem Universum ähnlich. Daraus können wir schließen, dass das Verhalten unserer Simulationskette korrekt ist. Aus diesem Ergebnis allein können wir jedoch nicht schließen, dass wir an einer Simulationskette teilnehmen.
• Die beiden Universen sind in ihrer Entwicklung, ihrer Struktur und ihrem Inhalt sehr unterschiedlich: Wiederum unter der Annahme, dass smin dem Universum ähnlich ist, aber beide einander unähnlich sind, ist sn-1 dem Universum unähnlich. Die Unähnlichkeit schließt die Entstehung von intelligentem Leben, das ein Universum simuliert, nicht aus. Das Ergebnis ist nicht schlüssig, da wir eine oder mehrere der folgenden Möglichkeiten in Betracht ziehen können:
  • Im weiteren Verlauf der Simulationskette hat eine Evolution stattgefunden, die die Unähnlichkeit verursacht hat.
  • Unsere Simulationskette simuliert ein Universum nicht korrekt, und der Fehler pflanzt sich in der Simulationskette fort.
  • Jedes simulierte Universum und das (simulierte oder nicht simulierte) Universum sind etwas Besonderes, denn entlang der Simulationskette ergibt sich in jeder der Simulationen ein anderes Verhalten, obwohl die Simulationen physikalisch korrekt sind.
  • Allein aufgrund der Unähnlichkeit können wir nicht feststellen, ob wir an einer Simulationskette teilnehmen.

 

VIII. SCHLUSSFOLGERUNG

Der Nachweis, dass wir nicht in einer Simulation leben, ist ein kompliziertes Unterfangen, das auf Theorie und Praxis der Informatik, Physik und Philosophie beruht. Aber wie immer sind die entscheidenden wissenschaftlichen Beweise nicht nur auf theoretischer Basis zu finden, sondern auch durch Experimente und Beobachtungen. Die Frage, ob wir in einer Simulation leben, ist offen. Mit den skizzierten Experimenten, Randbedingungen und vorgeschlagenen Beobachtungen hoffen wir, auf der Grundlage unserer wahrgenommenen und messbaren Realität Hinweise für oder gegen die Simulationshypothese zu erhalten.

Die sechs skizzierten Einschränkungen, die sich auf theoretische Informatik und Physik, experimentelle Beweise, Logik und Beobachtungen stützen, definieren die Grenzen, innerhalb derer eine universelle Simulation durchgeführt werden kann, wie z. B. die Unmöglichkeit, das Universum in vollem Umfang von innen zu simulieren. Die Beschränkungen hindern auch einen externen oder internen Programmierer daran, einen Computer zu bauen, der Teile des Universums genau simulieren kann, und damit eine Simulation zu konstruieren, die mit diesem identisch ist und – falls möglich – die Vorhersage der Zukunft ermöglichen würde. Während Alan Turing zeigte, was berechenbar ist, skizzieren wir, welche Computer konstruierbar sind und wie ein externer oder interner Programmierer die ultimativen Rechenressourcen nutzen kann, um ein Universum zu simulieren.

Wir alle sind Denker unserer Zeit, und in der Philosophie geht es heute oft darum, Richard Feynmans berühmtes “Kreidezitat” aus einem seiner Kurse – “Was ich nicht erschaffen kann, verstehe ich nicht” – wörtlich zu nehmen: Es ist eine Praxis des Denkens. Viele Menschen sind sich über grundlegende Überzeugungen und/oder Annahmen einig, z. B. dass die Mathematik die Syntax und Semantik des Universums ist, in der die ihm zugrunde liegende und bestimmende Physik ausgedrückt werden kann. Abstraktere Ideen, die sich auf solide wissenschaftliche Theorien und/oder Beweise stützen, besagen, dass die Quantenphysik zwar die “Maschinensprache” des Universums ist, dass aber viele Interpretationen möglich und rigoros sind, z. B. dass die ständig kollabierenden Wellenfunktionen der Teilchen zu einer unendlichen Anzahl von Paralleluniversen führen [9]. Abgesehen von der Quantenphysik ist es denkbar, dass wir in einer Raum-Zeit-Blase mit einem Durchmesser von 13,8 Milliarden Lichtjahren existieren, die anderen physikalischen Gesetzen unterliegt als andere Raum-Zeit-Blasen im Universum [86]. Jede physikalische Theorie ruht auf den Schultern von Giganten und umfasst eine Vielzahl von Ideen, die im Laufe der Zeit entstanden sind, sowie zahllose Fragen, die weiter untersucht werden müssen. Etwas Unerklärliches – in manchen Fällen sogar Mysteriöses – ist oft der Grund für menschliche Bemühungen und die Suche nach Antworten. In dieser Abhandlung haben wir aus einer “Es”-Perspektive heraus argumentiert, dass es etwas über die Realität zu entdecken gibt, unabhängig von den physikalischen Gesetzen, die sie regieren. Wir haben Experimente und Beobachtungen vorgeschlagen, die unsere wahrgenommene und gemessene physikalische Realität und die Berechenbarkeit innerhalb eines solchen formalen Systems betreffen. In der Physik ging es schon immer darum, über das Bekannte und Verstandene hinauszugehen. Ein Trend, der viele Formen annimmt, ist das Aufgeben etablierter physikalischer Gesetze und Theorien zugunsten der Suche nach einer neuen Physik des Universums. In diesem Papier haben wir jedoch eine klare Haltung zugunsten etablierter physikalischer Gesetze, Modelle und Theorien eingenommen, die zwar nicht experimentell bewiesen sind, aber auf der Grundlage unseres Verständnisses der Funktionsweise des Universums “vernünftig” erscheinen.

Die Autoren dieses Papiers erkennen an, dass Theorien, die besagen, dass das Bewusstsein grundlegend ist und dass die Realität eine Illusion ist, auf der alten Philosophie aufbauen, in der die Raumzeit eher wie ein Kopfhörer ist [87]. Solche Theorien besagen, dass unsere Erfahrungen real sind, beruhen aber auf der Vorstellung, dass das Bewusstsein die Grundlage unserer wahrgenommenen Realität ist und dass Körperlichkeit, Gedanken und Objekte entstehen können. Wenn das Bewusstsein grundlegend ist und Raum-Zeit, physikalische Gesetze und mathematische Strukturen organisch entstehen können – und wenn die Beweisbarkeit der Gesetze der Quantenmechanik auf eine solche Realität projiziert werden kann -, dann muss es zum Beispiel in der Macht eines externen Programmierers liegen, die Entropie anzuhalten und/oder umzukehren. Doch selbst wenn man die grundlegendste Annahme einer solchen Theorie – das universelle Bewusstsein – in Betracht zieht, wird in dieser Abhandlung nicht versucht, dafür oder dagegen zu argumentieren, da dies für Folgestudien offen gelassen wurde.

Die vorgeschlagenen Experimente beruhen auf mehreren Annahmen, die unser heutiges vorläufiges Verständnis der Naturgesetze ausmachen, einschließlich der Gesetze der Quantenphysik, die den grundlegendsten physikalischen Gesetzen entsprechen. In diesem Beitrag haben wir dargelegt, dass im Rahmen der derzeitigen Möglichkeiten der Computerphysik und unseres Verständnisses davon, wie eine Simulationshypothese im Rahmen unseres derzeitigen Verständnisses der Quantentheorie zum Leben erweckt werden könnte, bestimmte Grenzen bestehen. Dennoch argumentieren wir in Anlehnung an den Gödelschen Unvollständigkeitssatz und das von Alan Turing skizzierte Halting-Problem, dass ein Fortschritt immer möglich ist. Wenn es um die philosophische Frage der Schöpfung geht – sei es von der Einfachheit zur Komplexität oder von digitalen Entitäten (dem Bit) zur physikalisch wahrgenommenen Realität (dem “Es”) – liegt immer die Annahme zugrunde, dass “etwas” existiert. In jedem formalen System muss es einen Ausgangspunkt oder eine Begrenzung geben, aus der der Fortschritt folgt. Ohne die Annahme mindestens einer Vorbedingung ist ein wissenschaftliches Unterfangen unmöglich. Daher soll dieser Beitrag eine Diskussion über die Einbeziehung der skizzierten Zwänge und Einschränkungen in solide Theorien und Experimente anregen, anstatt für eine endgültige Lösung der Simulationshypothese zu plädieren. Diese Erfahrung beweist auch, dass der Reduktionismus als grundlegender wissenschaftlicher Ansatz zwar zu keiner schlüssigen Theorie über die Realität führt, aber innerhalb des gegebenen Rahmens funktioniert. Es gibt noch viel Arbeit in Bezug auf viele der heute akzeptierten Narrative. In verschiedenen Formen führen die quantenphysikalischen Gesetze zur physikalischen Vorhersagebeschränkung, durch die die grundlegendsten Gesetze eine exakte Simulation und damit eine Vorhersage verhindern. Die Befürworter eines deterministischen Universums lehnen den Nichtdeterminismus der Quantenphysik, auf dem einige der skizzierten Beschränkungen beruhen, entschieden ab; zwei der bekanntesten Vorschläge für den Determinismus sind der Superdeterminismus und die deterministische Quantenmechanik. Wir argumentieren logisch gegen beide Theorien und zeigen, warum sie keine ausreichenden Argumente für ein deterministisches Universum und gegen den freien Willen sind. Das Nachdenken über Simulationen ist dennoch fruchtbar, da andere Wege als die exakte Simulation des Universums zur Erforschung offen stehen. Die Simulation eines Universums – eine Simulation, die kleiner ist als der Computer, auf dem sie läuft, und denselben physikalischen Gesetzen unterliegt wie das Universum – ist möglich. In einer solchen Simulation kann intelligentes Leben – und hier weisen wir darauf hin, dass unsere Definitionen sowohl von Intelligenz als auch von Leben sicherlich unvollständig sind und dass Leben im Allgemeinen nicht unbedingt dem menschlichen Leben in Zusammensetzung und Verhalten ähnlich sein muss, um als solches zu gelten -, das ein Universum simuliert, entstehen oder von einem externen Programmierer künstlich eingeführt werden, was die Grundlage für das hier beschriebene Simulationskettenexperiment darstellt. Angenommen, eine Simulationskette entsteht in einer solchen Simulation. In diesem Fall muss dies nicht zwangsläufig zu der Schlussfolgerung führen, dass wir selbst bereits an einer Simulationskette beteiligt sind, was bedeutet, dass das Universum eine Simulation ist. Wie in der dritten Einschränkung der Berechenbarkeit dargelegt, ist jede Simulation in der Simulationskette weniger komplex als die vorhergehende, da die letztere den Computer einschließen muss, auf dem die erste läuft. Darüber hinaus wird jede der Simulationen, unabhängig von ihrer Komplexität im Vergleich zu anderen Simulationen in der Kette, mit der Zeit rechnerisch komplexer, da die globale thermodynamische Entropie immer zunimmt, auch wenn die lokale thermodynamische Entropie abnimmt, wenn sich beispielsweise astronomische Objekte bilden oder Leben entsteht. Die zunehmende thermodynamische Entropie erhöht die Komplexität, da die Teilcheninteraktionen und die Anzahl der Konfigurationen, die Teilchen annehmen können, entlang des Pfeils der Zeit zunehmen. Mit zunehmender Komplexität steigt zwangsläufig auch die Rechenkomplexität, und es werden mehr Rechenressourcen benötigt. Da alle Rechenressourcen endlich sind, kommen jedes Mal, wenn die Ressourcen eines Simulationsrechners erschöpft sind, alle Simulationen in der Kette zum Stillstand. Wir schlagen Ideen vor, wie ein externer Programmierer die Erschöpfung der Rechenressourcen vorübergehend umgehen kann, von denen einige im Universum durch Experimente oder Beobachtungen nachweisbar sein könnten. Nichts hindert einen externen Programmierer an grundlegenden und schwerwiegenden physikalischen Eingriffen in eine Simulationskette, wie z. B. eine Umkehrung der globalen thermodynamischen Entropie, die Verdichtung der Dimensionen, die Umsetzung des holographischen Prinzips in verschiedenen Formen oder ein absichtlicher Big Crunch. Angenommen, wir beobachten, dass eines oder mehrere dieser Szenarien – oder andere mit demselben Schweregrad – viele Male in der Simulationskette auftreten, und schließen daraufhin, dass die damit verbundenen Ereignisse statistisch relevant sind. In diesem Fall können wir daraus ableiten, dass es sich um ein erwartetes Verhalten handelt, und sollten wir auch im Universum Anzeichen dafür finden, können wir weiter folgern, dass wir an einer Simulationskette teilnehmen. Andere skizzierte Szenarien gehen davon aus, dass keine Simulationskette entstanden ist oder dass intelligentes Leben ein Universum simulieren will, sobald wir selbst ein Universum simulieren, was unterschiedliche Schlussfolgerungen darüber zulässt, ob wir in einer Simulation existieren. Bei einem der beschriebenen Experimente geht es schließlich darum, eine Simulation zu starten, die so komplex ist, dass intelligentes Leben mit der Absicht, ein Universum zu simulieren, entsteht, und diese Simulation mit der am wenigsten komplexen Simulation in einer Simulationskette zu vergleichen, in der intelligentes Leben noch die Absicht hat, ein Universum zu simulieren. Wenn die Ergebnisse ähnlich sind, können wir zu dem Schluss kommen, dass die von uns erstellte Simulationskette korrekt ist, aber es bedeutet auch, dass unsere derzeitige Wissensbasis nicht schlüssig ist und weitere Untersuchungen erfordert. Sechzig Jahre nach Asimovs “letzter Frage” sind wir mit der Unheilserklärung von Raum und Zeit, verschiedenen Ansichten über mögliche Multiversen, verstreuten Interpretationen der Quantenmechanik und einer Welt konfrontiert, in der die Mathematik zur spirituellen Kathedrale vieler Glaubenssysteme wird. Der Begriff der Schöpfung selbst bleibt eine offene philosophische Frage, ebnet aber dennoch den Weg für wissenschaftlichen Fortschritt durch weitere Erfahrungen und Fortschritte in der Quantentechnologie.

Mit anderen Worten, es bleibt noch Raum für eine letzte Frage. Wir freuen uns auf Ihre Überlegungen und eine spannende Diskussion: Es werde Licht.

 

 

 

 

 

VERWEISE

1. J. Rogan and E. Musk, “Joe rogan experience 1169 – elon musk.”

[Online]. Available: https://www.youtube.com/watch?v=ycPr5-27vSI

1. C. Nice and N. deGrasse Tyson, “Neil degrasse tyson explains the simulation hypothesis.” [Online]. Available: https://www.youtube.com/ watch?v=pmcrG7ZZKUc
2. D. J. Chalmers, “The matrix as metaphysics,” Science Fiction and Philosophy: From Time Travel to Superintelligence, pp. 35–54, 2016.
3. D. Falk, “The simulated world according to david chalmers.” [Online]. Available: https://nautil.us/ the-simulated-world-according-to-david-chalmers-238417/
4. N. Bostrom, “The simulation argument: Why the probability that you are living in a matrix is quite high,” Times Higher Education Supplement, 2003.
5. N. Bostrom, “Are we living in a computer simulation?” The philosophical quarterly, vol. 53, no. 211, pp. 243–255, 2003.
6. S. Hossenfelder, “The simulation hypothesis is pseudoscience.” [Online]. Available: https://www.youtube.com/watch?v=HCSqogSPU Q
7. J. Horgan, “Does quantum mechanics rule out free will?” [Online]. Available: https://www.scientificamerican.com/article/ does-quantum-mechanics-rule-out-free-will/
8. B. S. DeWitt and N. Graham, The many-worlds interpretation of quantum mechanics. Princeton University Press, 2015, vol. 63.
9. A. M. Turing et al., “On computable numbers, with an application to the entscheidungsproblem,” J. of Math, vol. 58, no. 345-363, p. 5, 1936.
10. B. Graham Dempsey and A. Bard, “Metamodern spirituality — syntheism, development, and the god event (w/ alexander bard).” [Online]. Available: https://www.youtube.com/watch?v=BmV9tdYyUUE
11. B. Weatherson, “Are you a sim?” The Philosophical Quarterly, vol. 53, no. 212, pp. 425–431, 2003.
12. S. Carroll, “Maybe we do not live in a simulation: The resolution conundrum,” Preposterous Universe, 2016.
13. B. Dainton, “On singularities and simulations,” Journal of Consciousness Studies, vol. 19, no. 1-2, pp. 42–85, 2012.
14. N. Tiku, “The google engineer who thinks the company’s ai has come to life.” [Online]. Available: https://www.washingtonpost.com/ technology/2022/06/11/google-ai-lamda-blake-lemoine/
15. R. Penrose and N. D. Mermin, “The emperor’s new mind: Concerning computers, minds, and the laws of physics,” 1990.
16. C. M. Kerskens and D. L. Perez, “Experimental indications of nonclassical brain functions,” Journal of Physics Communications, 2022.
17. D. J. Chalmers, “Facing up to the problem of consciousness,” Journal of consciousness studies, vol. 2, no. 3, pp. 200–219, 1995.
18. S. Hossenfelder, “The simulation hypothesis is pseudoscience.” [Online]. Available: http://backreaction.blogspot.com/2021/ 02/the-simulation-hypothesis-is.html
19. F. Singleton, “Grid length and resolution in weather prediction.” [Online]. Available: https://weather.mailasail.com/Franks-Weather/ Grid-Length-Resolution
20. R. P. Feynman, “Simulating physics with computers,” in Feynman and computation. CRC Press, 2018, pp. 133−−153.
21. A. Salam and J. C. Ward, “Electromagnetic and weak interactions,” IMPERIAL COLL OF SCIENCE AND TECHNOLOGY LONDON

(ENGLAND), Tech. Rep., 1964.

1. A. Salam, “Weak and electromagnetic interactions,” in Selected Papers Of Abdus Salam: (With Commentary). World Scientific, 1994, pp. 244– 254.
2. H. D. Politzer, “Asymptotic freedom: An approach to strong interactions,” Physics Reports, vol. 14, no. 4, pp. 129–180, 1974.
3. C. Rovelli, Quantum gravity. Cambridge university press, 2004.
4. ——, “Loop quantum gravity,” Living reviews in relativity, vol. 11, no. 1, pp. 1–69, 2008.
5. C. Kiefer, “Why quantum gravity?” in Approaches to fundamental physics. Springer, 2007, pp. 123–130.
6. C. P. Burgess, “Quantum gravity in everyday life: General relativity as an effective field theory,” Living Reviews in Relativity, vol. 7, no. 1, pp. 1–56, 2004.
7. D. G. Boulware and S. Deser, “Classical general relativity derived from quantum gravity,” Annals of Physics, vol. 89, no. 1, pp. 193–240, 1975.
8. J. Preskill, “Quantum computing in the nisq era and beyond,” Quantum, vol. 2, p. 79, 2018.
9. N. A. of Sciences Engineering, Medicine et al., “Quantum computing: progress and prospects,” 2019.
10. S.-S. Li, G.-L. Long, F.-S. Bai, S.-L. Feng, and H.-Z. Zheng, “Quantum computing,” Proceedings of the National Academy of Sciences, vol. 98, no. 21, pp. 11847–11848, 2001.
11. J. P. Dowling and G. J. Milburn, “Quantum technology: the second quantum revolution,” Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, vol. 361, no. 1809, pp. 1655–1674, 2003.
12. R. Healey, The quantum revolution in philosophy. Oxford University Press, 2017.
13. I. H. Deutsch, “Harnessing the power of the second quantum revolution,” PRX Quantum, vol. 1, no. 2, p. 020101, 2020.
14. N. Gisin, G. Ribordy, W. Tittel, and H. Zbinden, “Quantum cryptography,” Reviews of modern physics, vol. 74, no. 1, p. 145, 2002.
15. S. Pirandola, U. L. Andersen, L. Banchi, M. Berta, D. Bunandar, R. Colbeck, D. Englund, T. Gehring, C. Lupo, C. Ottaviani et al., “Advances in quantum cryptography,” Advances in optics and photonics, vol. 12, no. 4, pp. 1012–1236, 2020.
16. D. J. Bernstein and T. Lange, “Post-quantum cryptography,” Nature, vol. 549, no. 7671, pp. 188–194, 2017.
17. Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferova, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. Sawaya´ et al., “Quantum chemistry in the age of quantum computing,” Chemical reviews, vol. 119, no. 19, pp. 10856–10915, 2019.
18. B. Bauer, S. Bravyi, M. Motta, and G. K.-L. Chan, “Quantum algorithms for quantum chemistry and quantum materials science,” Chemical Reviews, vol. 120, no. 22, pp. 12685–12717, 2020.
19. M. Perelshtein, A. Sagingalieva, K. Pinto, V. Shete, A. Pakhomchik, A. Melnikov, F. Neukart, G. Gesek, A. Melnikov, and V. Vinokur, “Practical application-specific advantage through hybrid quantum computing,” arXiv preprint arXiv:2205.04858, 2022.
20. M. P. Harrigan, K. J. Sung, M. Neeley, K. J. Satzinger, F. Arute, K. Arya, J. Atalaya, J. C. Bardin, R. Barends, S. Boixo et al., “Quantum approximate optimization of non-planar graph problems on a planar superconducting processor,” Nature Physics, vol. 17, no. 3, pp. 332– 336, 2021.
21. S. Feld, C. Roch, T. Gabor, C. Seidel, F. Neukart, I. Galter, W. Mauerer, and C. Linnhoff-Popien, “A hybrid solution method for the capacitated vehicle routing problem using a quantum annealer,” Frontiers in ICT, vol. 6, p. 13, 2019.
22. M. Streif, F. Neukart, and M. Leib, “Solving quantum chemistry problems with a d-wave quantum annealer,” in International Workshop on Quantum Technology and Optimization Problems. Springer, 2019, pp. 111–122.
23. F. Neukart, D. Von Dollen, C. Seidel, and G. Compostella, “Quantum-enhanced reinforcement learning for finite-episode games with discrete state spaces,” Frontiers in physics, vol. 5, p. 71, 2018.
24. F. Neukart and S.-A. Moraru, “On quantum computers and artificial neural networks,” Journal of Signal Processing Research, vol. 2, p. 1, 2013.
25. S. Yarkoni, A. Alekseyenko, M. Streif, D. Von Dollen, F. Neukart, and T. Back, “Multi-car paint shop optimization with quantum annealing,” in 2021 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE, 2021, pp. 35–41.
26. “Das Flachheits-Problem.” [Online]. Available: https://www.scinexx.de/ dossierartikel/das-flachheits-problem/
27. “Orbital shapes.” [Online]. Available: https://energywavetheory.com/ atoms/orbital-shapes/
28. “M4: Spherical harmonics.” [Online]. Available: https://chem.libretexts.org/Ancillary Materials/Reference/Reference Tables/Mathematical Functions/M4%3A Spherical Harmonics
29. “Spherical harmonics.” [Online]. Available: https://chem.libretexts. org/Bookshelves/Physical and Theoretical Chemistry Textbook Maps/Supplemental Modules Physical and Theoretical Chemistry/

Quantum Mechanics/07. Angular Momentum/Spherical Harmonics

1. J. D. Bekenstein, “Generalized second law of thermodynamics in blackhole physics,” Physical Review D, vol. 9, no. 12, p. 3292, 1974.
2. D. Christodoulou, “Reversible and irreversible transformations in blackhole physics,” Physical Review Letters, vol. 25, no. 22, p. 1596, 1970.
3. S. W. Hawking, “Gravitational radiation from colliding black holes,” Physical Review Letters, vol. 26, no. 21, p. 1344, 1971.
4. C. E. Shannon, “A mathematical theory of communication,” The Bell system technical journal, vol. 27, no. 3, pp. 379–423, 1948.
5. J. D. Bekenstein, “Universal upper bound on the entropy-to-energy ratio for bounded systems,” Physical Review D, vol. 23, no. 2, p. 287, 1981.
6. J. Beckenstein, “Information in the holographic universe: Theoretical results about black holes suggest that the universe could be like a gigantic hologram,” Scientific American, 2003.
7. R. Bousso, “The holographic principle,” Reviews of Modern Physics, vol. 74, no. 3, p. 825, 2002.
8. G. Hooft, “The holographic principle,” in Basics and Highlights in Fundamental Physics. World Scientific, 2001, pp. 72–100.
9. R. P. Feynman, QED: The strange theory of light and matter. Princeton University Press, 2006, vol. 90.
10. S. Hossenfelder and T. Palmer, “Rethinking superdeterminism,” Frontiers in Physics, vol. 8, p. 139, 2020.
11. P. Mutalik, “How randomness can arise from determinism.” [Online]. Available: https://www.quantamagazine.org/ how-randomness-can-arise-from-determinism-20191014/
12. F. Morrison, The art of modeling dynamic systems: forecasting for chaos, randomness and determinism. Courier Corporation, 2012.
13. J. L. Park, “The concept of transition in quantum mechanics,” Foundations of physics, vol. 1, no. 1, pp. 23–33, 1970.
14. W. K. Wootters and W. H. Zurek, “A single quantum cannot be cloned,” Nature, vol. 299, no. 5886, pp. 802–803, 1982.
15. D. Dieks, “Communication by epr devices,” Physics Letters A, vol. 92, no. 6, pp. 271–272, 1982.
16. A. J. Leggett, B. Ruggiero, and P. Silvestrini, Quantum Computing and Quantum Bits in Mesoscopic Systems. Springer, 2004.
17. J. Dargan, “Top 63 quantum computer simulators for 2022.” [Online]. Available: https://thequantuminsider.com/2022/06/14/ top-63-quantum-computer-simulators-for-2022/
18. J. S. Bell, “Free variables and local causality,” in John S Bell On The Foundations Of Quantum Mechanics. World Scientific, 2001, pp. 84– 87.
19. G. Hooft, “A mathematical theory for deterministic quantum mechanics,” in Journal of Physics: Conference Series, vol. 67, no. 1. IOP Publishing, 2007, p. 012015.
20. P. C. W. Davies and J. R. Brown, The ghost in the atom: a discussion of the mysteries of quantum physics. Cambridge University Press, 1993.
21. B. Hensen, H. Bernien, A. E. Dreau, A. Reiserer, N. Kalb, M. S. Blok,´ J. Ruitenberg, R. F. Vermeulen, R. N. Schouten, C. Abellan´ et al., “Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres,” Nature, vol. 526, no. 7575, pp. 682–686, 2015.
22. “Observable universe contains ten times more galaxies than previously thought.” [Online]. Available: https://esahubble.org/news/heic1620/#2 [74] S. Hawking, The illustrated a brief history of time. Bantam, 1996.

1. P. J. E. Peebles, D. N. Schramm, E. L. Turner, and R. G. Kron, “The evolution of the universe,” Scientific American, vol. 271, no. 4, pp. 52– 57, 1994.
2. J. Khoury, B. A. Ovrut, N. Seiberg, P. J. Steinhardt, and N. Turok, “From big crunch to big bang,” Physical Review D, vol. 65, no. 8, p. 086007, 2002.
3. P. Horava and E. Witten, “Eleven-dimensional supergravity on a manifold with boundary,” Nuclear Physics B, vol. 475, no. 1-2, pp. 94–114, 1996.
4. P. Horava and E. Witten, “Heterotic and type I string dynamics from eleven dimensions,” in The World in Eleven Dimensions: Supergravity, Supermembranes and M-theory. CRC Press, 1999, pp. 397–415.
5. T. Banks, W. Fischler, S. H. Shenker, and L. Susskind, “M theory as a matrix model: A conjecture,” in The World in Eleven Dimensions: Supergravity, Supermembranes and M-theory. CRC Press, 1999, pp. 435–451.
6. M. Kaku, Introduction to superstrings and M-theory. Springer Science & Business Media, 2012.
7. M. J. Duff, “The theory formerly known as strings,” Scientific American, vol. 278, no. 2, pp. 64–69, 1998.
8. I. Bengtsson, “Anti-de sitter space,” Lecture notes, vol. 118, 1998.
9. E. Witten, “Anti de sitter space and holography,” arXiv preprint hepth/9802150, 1998.
10. O. Aharony, S. S. Gubser, J. Maldacena, H. Ooguri, and Y. Oz, “Large n field theories, string theory and gravity,” Physics Reports, vol. 323, no. 3-4, pp. 183–386, 2000.
11. A. S. Chou, R. Gustafson, C. Hogan, B. Kamai, O. Kwon, R. Lanza, L. McCuller, S. S. Meyer, J. Richardson, C. Stoughton et al., “First measurements of high frequency cross-spectra from a pair of large michelson interferometers,” Physical review letters, vol. 117, no. 11, p. 111102, 2016.
12. M. Tegmark, “Parallel universes,” Scientific American, vol. 288, no. 5, pp. 40–51, 2003.
13. D. Hoffman, The case against reality: Why evolution hid the truth from our eyes. WW Norton & Company, 2019.